728x90
특성 공학(feature engineering)
- 기존의 특성을 사용해 새로운 특성을 만들어내는 작업
- 특성 공학 기법
- 차원 축소(Dimension Reduction)
- 특성 선정(Feature Selection)
- 특성 랭킹 또는 특성 중요도에 따라 선정
- 분석가의 사전 배경 지식을 이용하거나, 랜덤 선정 및 측정을 반복하는 방법
- 특성 추출(Feature Extraction)
- 특성들의 조합으로 새로운 특성을 생성
- 특성 선정(Feature Selection)
- 스케일링(Scaling)
- 변수의 분포가 편향되어 있을 경우, 변수 간의 관계가 잘 드러나지 않는 경우 범위 변환
- 변형(Transform)
- 기존에 존재하는 변수의 성질을 이용해 다른 변수를 생성하는 방법
- 예) 날짜별 데이터에 주말 여부 추가
- 기존에 존재하는 변수의 성질을 이용해 다른 변수를 생성하는 방법
- 비닝(Binning) ※Bin:구간->구간화 한다
- 연속형 변수를 범주형 변수로 변환
- 예) 33세, 47세 -> 30대, 40대
- 연속형 변수를 범주형 변수로 변환
- 더미(Dummy)
- 범주형 변수를 연속형 변수로 변환
- 기존 특성이나 특성의 조합을 규칙에 따라 수치화하여 추가
- 차원 축소(Dimension Reduction)
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.linear_model import LinearRegression, Ridge, Lasso
import matplotlib.pyplot as plt
01. 데이터 준비
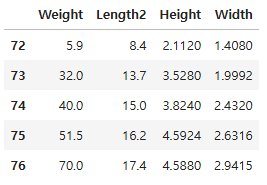
df = pd.read_csv("./data/Fish.csv")
df = df.loc[df["Species"] == "Perch", ["Weight", "Length2", "Height", "Width"]]
df.head()
x = df.drop("Weight", axis = 1)
y = df["Weight"]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, random_state =24)
x_train.shape, x_test.shape
((42, 3), (14, 3))
# PolynomialFeatures 사용 예시
pf = PolynomialFeatures()
pf.fit_transform([[2, 3]])
# 상수항, 기존컬럼1, 기존컬럼2, .. 상수항은 y절편을 표시하기 위해 필요
array([[1., 2., 3., 4., 6., 9.]])
# 특성이 어떻게 만들어졌는지 확인
pf.get_feature_names_out()
array(['1', 'x0', 'x1', 'x0^2', 'x0 x1', 'x1^2'], dtype=object)
- include_bias : 절편을 추가해주는 파라미터
- 사이킷런의 선형 회귀 모델은 자동으로 절편을 추가해주기 때문에 굳이 절편을 추가할 필요가 없음
pf = PolynomialFeatures(include_bias = False)
pf.fit_transform([[2, 3]])
array([[2., 3., 4., 6., 9.]])
# 실전 적용
pf = PolynomialFeatures(include_bias = False)
poly_train = pf.fit_transform(x_train)
poly_test = pf.transform(x_test)
- PolynomialFeatures 는 별도의 통계값을 저장하지 않기 때문에 테스트 세트를 함께 변환해도 차이가 없지만 항상 훈련 데이터를 기준으로 학습하고 테스트데이터를 변환하는 습관을 들이는 것이 중요
poly_train.shape
(42, 9)
02. 모델 훈련
# 특성공학 전 데이터로 학습한 모델
lr_org = LinearRegression()
lr_org.fit(x_train, y_train)
print(lr_org.score(x_train, y_train))
print(lr_org.score(x_test, y_test))
0.9413243113426596
0.9222008291291192
lr_poly = LinearRegression()
lr_poly.fit(poly_train, y_train)
print(lr_poly.score(poly_train, y_train))
print(lr_poly.score(poly_test, y_test))
0.9917700872190389
0.9530888492126584
03. 모델 최적화
- 특성을 더 추가
- degree 매개변수: 고차항의 최대 차수를 지정
pf = PolynomialFeatures(degree = 5, include_bias = False)
poly_train5 = pf.fit_transform(x_train)
poly_test5 = pf.transform(x_test)
poly_train5.shape
(42, 55)
lr_poly5 = LinearRegression()
lr_poly5.fit(poly_train5, y_train)
print(lr_poly5.score(poly_train5, y_train))
print(lr_poly5.score(poly_test5, y_test))
0.9999999999998926
-576.637906098756- 훈련 데이터에 대해서는 완벽하게 학습했음
- 테스트 데이터에 대해서는 분산보다 오차가 큼
- 데이터의 평균으로 찍는 것 보다 성능이 떨어짐
- 과대적합이 일어났음
04. 규제(regularization)
- 머신러닝 모델이 훈련 세트를 과도하게 학습하지 못하도록 방지하는 것
- 선형 회귀 모델의 경우에는 특성의 기울기 크기를 제한
- 선형 회귀 모델에 규제를 가하는 방법에 따라 릿지(ridge)모델과 라쏘(lasso)모델로 나뉨
- 릿지 모델(제곱->2)
- 계수를 제곱한 값을 제한
- l2규제
- 라쏘 모델(|| 1처럼 생김)
- 계수의 절댓값을 제한
- l1규제
# 일반적으로 선형회귀 모델에 규제를 적용할 때 계수 값의 크기가 서로 많이 다르면 제어가 힘듦
# 규제 적용 전에 스케일링을 수행
ss = StandardScaler()
scaled_train = ss.fit_transform(poly_train5)
scaled_test = ss.transform(poly_test5)
05. 릿지 회귀
scaled_train.shape
(42, 55)
rid = Ridge()
rid.fit(scaled_train, y_train)
print(rid.score(scaled_train, y_train))
print(rid.score(scaled_test, y_test))
# 과대적합이 방지됨. 테스트 성능도 좋아짐
0.9911543511681574
0.9736289107835776
■ 초매개변수(hyperparameter)
- 머신러닝 모델이 학습할 수 없고 사람이 설정해야하는 파라미터
- 사이킷런 모델에서 하이퍼파라미터는 클래스의 매개변수로 표현됨
■ 릿지 모델 하이퍼파라미터 튜닝
- alpha : 규제의 강도
- alpha 값이 크면
- 규제의 강도가 세짐
- 계수의 값을 줄이고 과소적합을 유도
- alpha 값이 작으면
- 규제의 강도가 약해짐
- 계수의 값을 덜 줄이고 과대적합 가능성이 커짐
- alpha 값이 크면
# 디지털 노가다를 해야함
train_hist = []
test_hist = []
alpha_li = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_li:
# 모델 생성
rid = Ridge(alpha = alpha)
# 훈련
rid.fit(scaled_train, y_train)
# 모델 성능을 저장
train_hist.append(rid.score(scaled_train, y_train))
test_hist.append(rid.score(scaled_test, y_test))
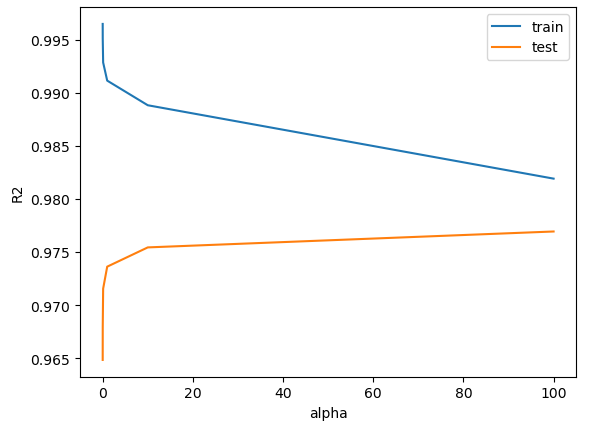
plt.figure()
plt.plot(alpha_li, train_hist)
plt.plot(alpha_li, test_hist)
plt.xlabel("alpha")
plt.ylabel("R2")
plt.legend(labels = ["train", "test"])
plt.show()
plt.figure()
# alpha 값을 그대로 x에 적용하면 간격이 서로 다르기 때문에 로그 함수로 바꾸어서 시각화
plt.plot(np.log10(alpha_li), train_hist)
plt.plot(np.log10(alpha_li), test_hist)
plt.xlabel("alpha")
plt.ylabel("R2")
plt.legend(labels = ["train", "test"])
plt.show()
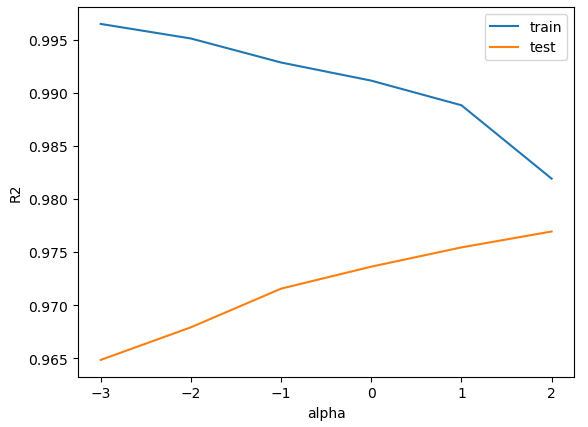
- alpha가 작을 때는 훈련데이터에만 잘 맞고 테스트 데이터에는 못 맞힘
- 과대적합이 일어났음
- alpha가 커질수록 훈련 데이터 점수가 낮아짐
- 과소적합으로 유도되고 있음
- 테스트 데이터에 가장 점수가 높은 alpha 값은 100임
rid = Ridge(alpha = 100)
rid.fit(scaled_train, y_train)
print(rid.score(scaled_train, y_train))
print(rid.score(scaled_test, y_test))
0.9819217522404685
0.9769424248340844
06. 라쏘 회귀
las = Lasso()
las.fit(scaled_train, y_train)
print(las.score(scaled_train, y_train))
print(las.score(scaled_test, y_test))
0.9905860936034936
0.9740948154378994
■ 라쏘 모델 하이퍼 파라미터 튜닝
# 디지털 노가다를 해야함
train_hist = []
test_hist = []
alpha_li = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_li:
# 모델 생성
las = Lasso(alpha = alpha)
# 훈련
las.fit(scaled_train, y_train)
# 모델 성능을 저장
train_hist.append(las.score(scaled_train, y_train))
test_hist.append(las.score(scaled_test, y_test))
plt.figure()
plt.plot(np.log10(alpha_li), train_hist)
plt.plot(np.log10(alpha_li), test_hist)
plt.xlabel("alpha")
plt.ylabel("R2")
plt.legend(labels = ["train", "test"])
plt.show()
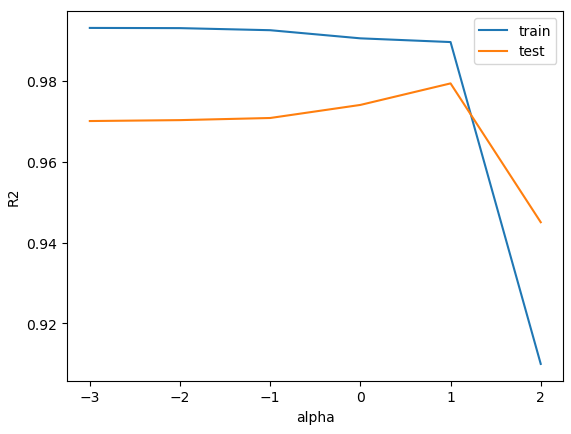
# 모델 성능이 가장 높은 지점 확인
las = Lasso(alpha = 10)
las.fit(scaled_train, y_train)
print(las.score(scaled_train, y_train))
print(las.score(scaled_test, y_test))
0.9896658708984675
0.9794258034118398
las.coef_
array([ 0. , 0. , 0. , 0. , 0. ,
89.41211883, 0. , 20.43220389, 3.31655753, 0. ,
14.54670432, 23.82109565, 54.72403388, 7.62332148, 0. ,
77.41683532, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 53.39922771,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ])
print(np.sum(las.coef_ == 0))
46
- 라쏘 모델은 기울기를 0으로 만드는 경우가 있음
- 현재는 46개의 독립변수의 기울기를 0으로 만들어 사용하지 않음
- 이런 특징을 이용해 유용한 특성을 선택하는 용도로도 사용할 수 있음
728x90
'08_ML(Machine_Learning)' 카테고리의 다른 글
| 12_야구선수 연봉_선형회귀 (1) | 2025.04.04 |
|---|---|
| 11_Ridge, Lasso, Elastic Net (0) | 2025.04.04 |
| 09_선형 회귀 실습 (0) | 2025.04.04 |
| 08_선형회귀 (0) | 2025.04.04 |
| 07_KNN구현(Numpy(넘파이)) (0) | 2025.04.04 |