728x90
선형회귀
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
df = pd.read_csv("./data/Fish.csv")
df = df.loc[df["Species"] == "Perch", ["Species", "Length2", "Weight"]]
df.head()
x_train, x_test, y_train, y_test = train_test_split(df["Length2"], df["Weight"], test_size = 0.25,
random_state = 23)
x_train = np.reshape(x_train.values, (-1, 1))
x_test = np.reshape(x_test.values, (-1, 1))
01. 선형 회귀(linear regression)
- 피쳐를 가장 잘 표현하는 하나의 직선을 학습하는 알고리즘 (데이터의 일반적인 패턴을 파악 예)y = ax + b)
- 장점
- 계수들에 대한 해석이 간단
- 학습과 예측 속도가 빠름
- 회귀식이 만들어져서 예측이 어떻게 됐는지 쉽게 이해할 수 있음
- 단점
- 데이터가 선형적이지 않을 경우 모델이 데이터에 적합하지 않을 수 있음
- 이상치에 민감
lr = LinearRegression()
# 선형회귀 모델 훈련
lr.fit(x_train, y_train)
# 50cm 농어에 대한 예측
lr.predict([[50]])
array([1180.93954674])
- 선형회귀 모델이 찾은 가장 적합한 직선은 lr 객체에 저장되어 있음
# 계수(coefficient), y절편
print(lr.coef_, lr.intercept_)
[35.83686955] -610.9039309395812
- 회귀식: 35.84 * Length2 + (-610.9)
- coef_ 와 intercept_ 처럼 머신러닝이 찾은 값을 모델 파라미터(model parameter) 라고 부름
- 즉, 머신러닝 알고리즘의 훈련 과정은 최적의 모델 파라미터를 찾는 것
- 선형 회귀와 같이 모델 파라미터를 훈련하는 것을 모델 기반 학습 이라고 하고, KNN과 같이 모델 파라미터가 없이 훈련 데이터를 저장하는 훈련 방법을 사례 기반 학습 이라고 함
50 * lr.coef_[0] + lr.intercept_
1180.939546737759
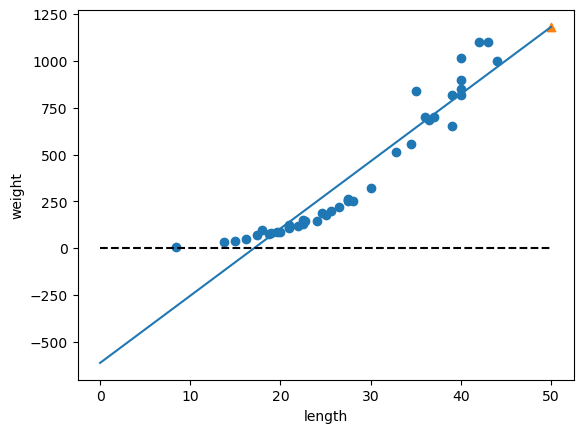
# 훈련 데이터와 회귀선 시각화
plt.figure()
plt.scatter(x_train, y_train)
plt.plot([0, 50], [lr.intercept_, 50 * lr.coef_[0] + lr.intercept_])
plt.scatter(50, 1180, marker = "^")
plt.plot([0, 50], [0, 0], "k--")
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
02. 모델 평가
lr.score(x_test, y_test)
0.962238206088814
pred = lr.predict(x_test)
mae = mean_absolute_error(y_test, pred)
mae
59.39567412291391
03. 다항 회귀
- 실제 농어의 무게는 일직선 이라기 보다는 왼쪽 위로 구부러진 곡선에 가깝기 때문에 직선보다는 곡선으로 예측하는 것이 더 적합
- 길이를 제곱한 항을 추가하여 2차 방정식의 그래프 형태로 학습
df["squared"] = df["Length2"] ** 2
df.head()
x_train, x_test, y_train, y_test = train_test_split(df[["Length2", "squared"]], df["Weight"],
test_size = 0.25, random_state =23)
lr = LinearRegression()
lr.fit(x_train, y_train)
lr.score(x_test, y_test)
0.9828804135599647
pred = lr.predict(x_test)
mae = mean_absolute_error(y_test, pred)
# 평균오차가 30.57으로 줆(독립변수가 늘어나면 종속변수에 대해 판단할 기준이 많아진다는 것이므로)
mae
30.56851982713119
# 50cm 농어에 대한 예측
lr.predict([[50, 2500]])
array([1597.75345786])
print(lr.coef_, lr.intercept_)
[-25.67925716 1.08528192] 168.5115152392617
- 회귀식: -25.68 * Length2 + 1.09 * squared + 168.51
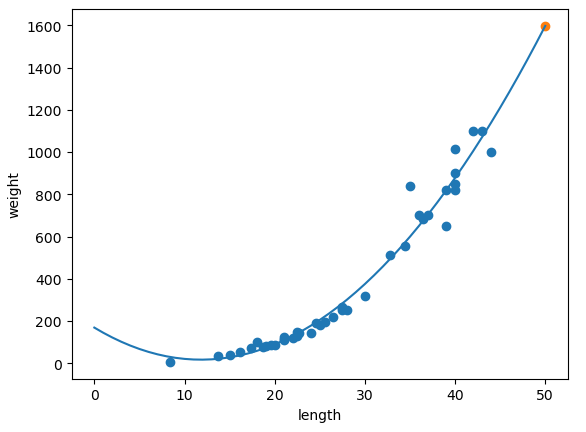
# 다항회귀 시각화
points = np.arange(51)
plt.scatter(x_train["Length2"], y_train)
plt.plot(points, lr.coef_[0] * points + lr.coef_[1] * (points ** 2) + lr.intercept_)
plt.scatter(50, 1597)
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
728x90
'08_ML(Machine_Learning)' 카테고리의 다른 글
| 10_다중 선형 회귀 규제 (0) | 2025.04.04 |
|---|---|
| 09_선형 회귀 실습 (0) | 2025.04.04 |
| 07_KNN구현(Numpy(넘파이)) (0) | 2025.04.04 |
| 06_KNN 심화 (0) | 2025.04.04 |
| 05_KNN회귀 (0) | 2025.04.04 |