728x90
군집모델_심화
k-means 클러스터링의 최적의 k값을 찾는 방법
- 비즈니스 도메인 지식
- 정성적인 선정 방법
- 데이터적인 근거는 다소 부족하지만, 클러스터링 자체가 해석을 통한 비즈니스 인사이트 도출이 주 목적이기 때문에 많은 프로젝트에서 이 방법을 사용
- 엘보우 기법(Elbow method)
- 군집 내 중심점과 관측치 간 거리 합(Inertia value)이 급감하는 구간의 k개수를 선정
- 군집의 수가 k였을 때보다 k + 1개일 때 거리합이 급감했다는 것은 유사한 속성의 관측치들끼리 잘 묶였다는것을 의미
- 따라서 k가 더 증가해도 거리합이 별로 줄어들지 않을 때는 k를 더 증가시킬 필요가 없다는 의미
- 이 때의 그래프 모양이 팔꿈치(Elbow) 형태를 하고 있기 때문에 엘보우 기법이라고 불림
- 실루엣 계수(Silhouette coefficient) 활용
- 실루엣 계수: 군집 안의 관측치들이 다른 군집과 비교해서 얼마나 비슷한지를 나타내는 수치
- 동일한 군집 안에 있는 관측치들 간의 평균 거리와 가장 가까운 다른 군집과의 평균 거리를 구해 실루엣 계수를 계산

- 동일한 군집 내 관측치들 간 평균 거리가 집단 간 평균 거리보다 짧을수록 실루엣 계수는 높아짐
- 범위는 -1부터 1사이의 값을 가지며 실루엣 계수가 1에 가까울수록 군집이 적합하게 나누어졌음을 의미
DBSCAN
- 아무리 k값을 잘 지정한다고 해도 데이터의 형태가 k-means 클러스터링 알고리즘에 적합하지 않으면 효과적인 군집화를 할 수가 없음
- 밀도 기반의 원리를 이용한 클러스터링 기법이 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
- DBSCAN은 별도의 k값 지정이 필요 없고 관측치들의 밀도를 통해 자동으로 적절한 군집 수를 찾음
- 밀도를 측정하려면 두 가지 기준이 필요
- 기준 관측치로부터 "이웃"한 관측치인지 구별할 수 있는 거리 기준(epsilon)이 필요
- 거리 기준값이 크면 데이터 공간상 멀리 있는 관측치도 이웃한 관측치로 인식
- 거리 기준 내에 포함된 이웃 관측치 수(minPts)에 대한 기준이 필요
- 특정 거리 안에 몇 개 이상의 관측치가 있어야 하나의 군집으로 판단할 것인가를 결정
- 기준 관측치로부터 "이웃"한 관측치인지 구별할 수 있는 거리 기준(epsilon)이 필요
- 밀도를 측정하려면 두 가지 기준이 필요
- 기준 밀도를 가진 관측치들을 기준으로 군집화를 하기 때문에 U자형과 같이 오복한 데이터나 H와 같은 모양의 데이터 분포도 효과적으로 군집화할 수 있고, 군집이 명확하지 않은 이상치를 잘 분류해낼 수 있음
- 하지만 k-means에 비해 필요한 연산량이 많고, 특히 독립변수가 늘어날 수록 필요한 연산량이 급증하기 때문에 변수를 적절히 설정해줘야 함
- 그리고 데이터 특성을 모를 경우에는 적절한 파라미터 값을 설정하는 것이 어려움
군집화 모델 분석
- 군집화 모델은 분류된 각 군집의 특성을 파악하여 군집에 이름을 붙여서 그 특징을 정의하는 작업이 무엇보다 중요
- 클러스터링에 사용한 독립변수들이 다른 군집들에 비해서 어떠한 특성을 가지고 있는지를 확인하여 각 군집을 명확하게 정의해야 함
- 그 다음 각 군집의 특성에 맞는 비즈니스 전략을 수립
- 각 군집에 어느 정도의 데이터가 할당 되었는지 확인하여, 특정 군집에 너무 많은 데이터가 쏠렸거나, 너무 적은 데이터가 할당되어 군집으로서 효율성이 떨어지는 군집은 없는지 확인
- 각 독립 변수들이 다른 군집 혹은 전체 평균과 얼마나 다른지 확인하여 군집의 특성을 파악
- 이를 통해 군집의 이름을 설정
- 특성이 확실하여 쉽게 정의할 수 있는 군집도 있지만, 별다른 특성이 없는 군집도 있을 수 있음
- 이 경우 무리해서 억지로 군집을 정의하기 보다는 비슷한 군집끼리 묶어서 "일반 고객"등으로 별도 분류하는 것도 하나의 방법
- 군집 간의 수치적 차이를 보다 확실하게 파악하기 위해서는 t-test나 ANOVA등을 통해 군집 간 평균값의 차이가 우연한 차이인지, 통계적으로 유의미한 차이인지 검증하는 절차를 거치를 것이 좋음
from yellowbrick.cluster import KElbowVisualizer, SilhouetteVisualizer
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans, DBSCAN
from sklearn.metrics import silhouette_score
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 경고 메세지 제거
import warnings
warnings.filterwarnings("ignore")
df = pd.read_csv("./data/Mall_Customers.csv")
df.head()

df.shape
(200, 5)
df.dtypes
CustomerID int64
Gender object
Age int64
Annual Income (k$) int64
Spending Score (1-100) int64
dtype: object
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 200 entries, 0 to 199
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 CustomerID 200 non-null int64
1 Gender 200 non-null object
2 Age 200 non-null int64
3 Annual Income (k$) 200 non-null int64
4 Spending Score (1-100) 200 non-null int64
dtypes: int64(4), object(1)
memory usage: 7.9+ KB
df.describe(include = "all")

# pairplot
df1 = df.drop("CustomerID", axis = 1)
sns.set_style("ticks")
sns.pairplot(df1, diag_kind = "kde", hue = "Gender", corner = True, height = 5)
plt.show()

- 각 변수 간의 관계를 파악하기 위해 산점도 행렬을 시각화하여 분포를 확인
- spending score 변수와 annual income 변수와의 관계에서 각 5개 정도의 군집이 나눠질 수 있을 것으로 보이지만 연령과 성별 변수도 함께 사용하여 군집화할 예정이므로 이러한 분포는 참고로만 사용
# Gender 변수 전처리
df2 = pd.get_dummies(df1, columns = ["Gender"], drop_first = True)
df2.head()
# 스케일링 이유: 거리기반의 알고리즘은 단위가 비슷해야하므로
# 데이터 정규화
mm = MinMaxScaler()
scaled_data = mm.fit_transform(df2)
scaled_data[:5]
array([[0.01923077, 0. , 0.3877551 , 1. ],
[0.05769231, 0. , 0.81632653, 1. ],
[0.03846154, 0.00819672, 0.05102041, 0. ],
[0.09615385, 0.00819672, 0.7755102 , 0. ],
[0.25 , 0.01639344, 0.39795918, 0. ]])- 거리 기반 군집화 알고리즘은 스케일링을 적용하는 것을 권장
# k-means 군집화 모델 생성
kmeans_model_1 = KMeans(n_clusters = 3, random_state = 26)
kmeans_model_1.fit(scaled_data)

# 각각의 클러스터가 중심까지 거리 제곱합
print(kmeans_model_1.inertia_)
29.63233438025291
# 클러스터 중심점의 좌표
print(kmeans_model_1.cluster_centers_)
[[1.92307692e-01 3.87205987e-01 6.51286602e-01 1.00000000e+00]
[3.86504121e-01 3.62704918e-01 5.15579446e-01 4.44089210e-16]
[6.68040293e-01 3.87002342e-01 3.02478134e-01 1.00000000e+00]]
# 반복 횟수
print(kmeans_model_1.n_iter_)
5
# 엘보우 차트 시각화
elbow_chart = KElbowVisualizer(kmeans_model_1, k = (1, 11),)
elbow_chart.fit(scaled_data)
elbow_chart.draw()
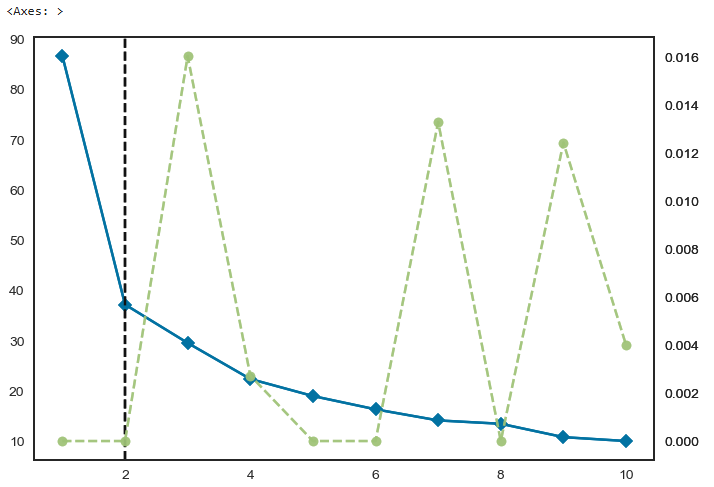
# 파란색선 : 이너셔
# 연두색선 : 학습시간
- 2 지점에서 경사가 급감하는 모습을 보이고 있음
- 성별 변수 때문일 것으로 예상
# 실루엣 계수 시각화 1
# 각 K의 실루엣 계수 저장
silhouette_coef = []
# 실루엣 계수 그래프 생성
for k in range(2, 11):
kmeans_silhouette = KMeans(n_clusters = k, random_state = 26)
kmeans_silhouette.fit(scaled_data)
score = silhouette_score(scaled_data, kmeans_silhouette.labels_)
silhouette_coef.append(score)
plt.plot(range(2, 11), silhouette_coef)
plt.xticks(range(2, 11))
plt.grid()
plt.xlabel("Number of Clusters")
plt.ylabel("silhouette Coefficient")
plt.show()
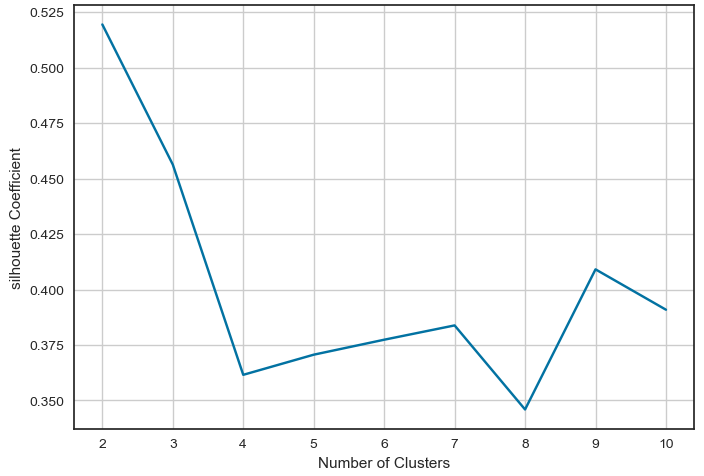
# 실루엣 계수 시각화 2
fig, ax = plt.subplots(3, 2, figsize = (15, 15))
for i in range(2, 8):
# k-means 군집화 모델 생성
kmeans_model_3 = KMeans(n_clusters = i, random_state = 26)
q, mod = divmod(i, 2)
# 실루엣 계수 시각화
visualizer = SilhouetteVisualizer(kmeans_model_3, colors = "yellowbrick", ax = ax[q-1][mod])
visualizer.fit(scaled_data)
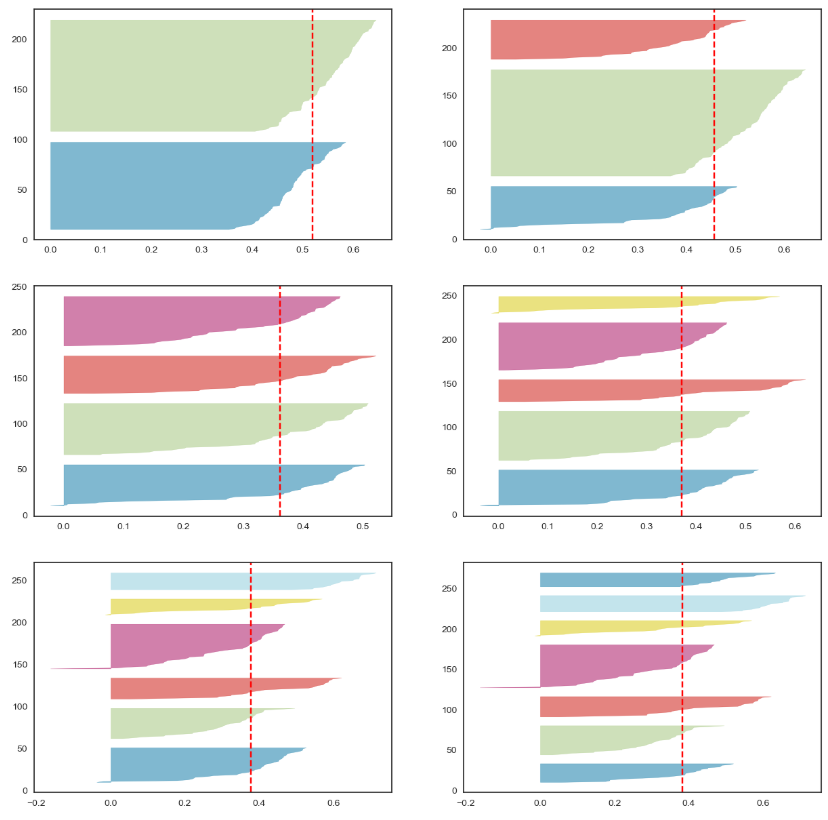
- 4개의 군집이 관측치가 비교적 균등하게 나뉘며 실루엣 계수의 편차도 고른 편
- 6개의 군집부터는 일부 실루엣 계수의 음수가 크게 나타남
kmeans_model_4 = KMeans(n_clusters = 4, random_state = 26)
# 군집 번호 결합
df2["cluster1"] = kmeans_model_4.fit_predict(scaled_data)
df2.head()
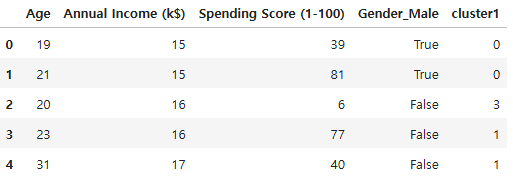
# 시각화
plt.figure(figsize = (8, 8))
for i in range(df2["cluster1"].max() + 1):
plt.scatter(df2.loc[df2["cluster1"] == i, "Annual Income (k$)"],
df2.loc[df2["cluster1"] == i, "Spending Score (1-100)"],
label = "cluster" + str(i))
plt.legend()
plt.title("K means visualization", size = 12)
plt.xlabel("Annual Income (k$)", size = 10)
plt.ylabel("Spending Score (1-100)", size = 10)
plt.show()

- 4개의 군집으로 나눈 군집의 분포를 확인하기 위해 annual income 변수를 x축으로, spending score변수를 y축으로 설정하여 시각화
# DBSCAN 모델 생성
dbscan_model = DBSCAN(eps = 0.7, min_samples = 5)
# 군집화 모델 학습 및 클러스터 예측 결과 반환
dbscan_model.fit(scaled_data)
df2["cluster2"] = dbscan_model.fit_predict(scaled_data)
# 시각화
plt.figure(figsize = (8, 8))
for i in range(df2["cluster2"].max() + 1):
plt.scatter(df2.loc[df2["cluster2"] == i, "Annual Income (k$)"],
df2.loc[df2["cluster2"] == i, "Spending Score (1-100)"],
label = "cluster" + str(i))
plt.legend()
plt.title("DBSCAN visualization", size = 12)
plt.xlabel("Annual Income (k$)", size = 10)
plt.ylabel("Spending Score (1-100)", size = 10)
plt.show()
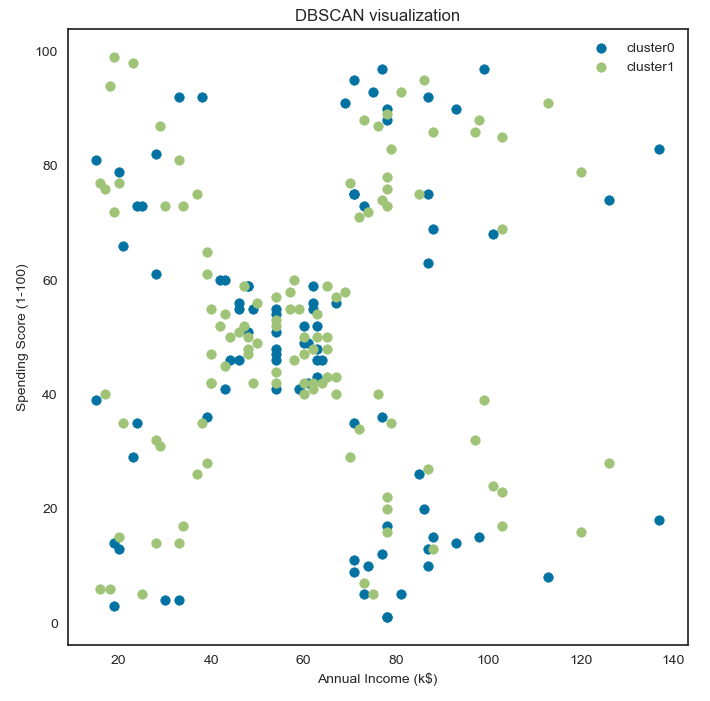
- 밀도 기반의 DBSCAN 모델은 군집 수가 자동으로 설정
- 관측치 간의 거리를 설정하는 eps 옵션과 한 군집에 속하는 최소 관측치 수를 설정하는 min_samples 옵션을 통해 군집 수를 간접적으로 조정할 수 있음
# k-means 군집 별 특성 확인
df_kmeans = df2.groupby("cluster1").mean()
df_kmeans["cnt"] = df2.groupby("cluster1")["Age"].count()
df_kmeans

# pd.DataFrame(df2.mean())
df2.mean()
Age 38.85
Annual Income (k$) 60.56
Spending Score (1-100) 50.20
Gender_Male 0.44
cluster1 1.53
cluster2 0.56
dtype: float64
# DBSCAN 군집 별 특성 확인
df_dbscan = df2.groupby("cluster2").mean()
df_dbscan["cnt"] = df2.groupby("cluster2")["Age"].count()
df_dbscan

- dbscan 모델의 경우 성별에 따라 두 개의 군집으로 나뉘어 졌음
- 성별이 범주형 변수이기 때문에 변별력이 강해서 다른 변수의 영향력을 압도한 것으로 보임
- 비즈니스적으로 의미 있는 군집을 만들기 위해서는 성별 변수를 제거하거나 다른 변수를 추가해야함
728x90
'08_ML(Machine_Learning)' 카테고리의 다른 글
| 29_군집분석_연습문제 (0) | 2025.04.14 |
|---|---|
| 28_주 성분 분석 (0) | 2025.04.14 |
| 26_군집 알고리즘(k-means) (0) | 2025.04.11 |
| 25_군집 알고리즘(비지도 학습)-과일 사진 레이블 없이 분류 (0) | 2025.04.11 |
| 24_파이프라인 구축 (0) | 2025.04.11 |