728x90
군집 알고리즘(k-means)
k-means(k-평균) 군집 알고리즘
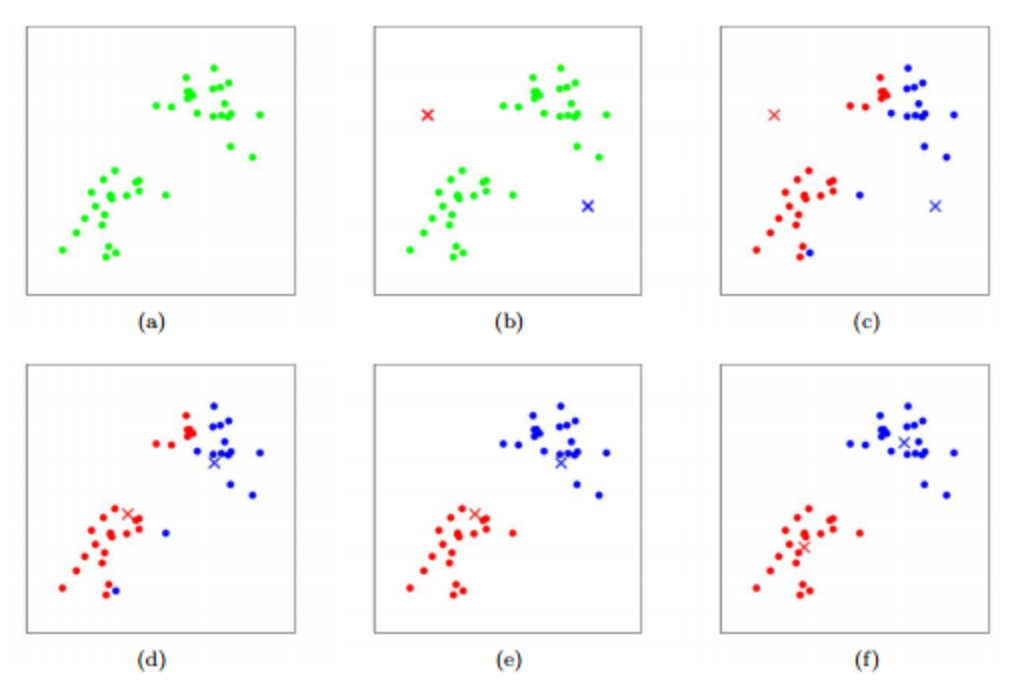
- 작동 방식
- 무작위로 k개의 클러스터 중심을 정함(b)
- 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정(c, e)
- 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경(d, f)
- 클러스터 중심에 변화가 없을 때까지 2 ~ 3 번 과정을 반복
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
fruits = np.load("./data/fruits_300.npy")
fruits_2d = fruits.reshape(-1, 100 * 100)
fruits.shape, fruits_2d.shape
((300, 100, 100), (300, 10000))
# kmeans 모델 생성
km = KMeans(n_clusters = 3, random_state = 26)
# n_clusters: k ->군집 중심점을 몇개 쓸것인가 기본값은 8
# 초기값을 어떻게 설정하는가 에 따라 영향을 많이 받음 하나의 군집중심점이 정해지면 그로부터 시작
# 초기값을 첫번째 중심점으로부터 가능한 한 멀리설정하면 오분류를 방지할 수 있다
km.fit(fruits_2d)
# 군집 결과 확인(각 샘플이 어떤 레이블에 해당되는지)
print(km.labels_)
[0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 2 0 2 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 0 2 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1]
- 레이블값에는 아무런 의미가 없음
- 각 레이블이 어떤 과일을 의미하는지 알아보려면 직접 이미지를 확인해야함
# 각 레이블로 모인 샘플 개수 확인
print(np.unique(km.labels_, return_counts = True))
(array([0, 1, 2]), array([ 90, 98, 112], dtype=int64))
# 각 클러스터가 어떤 데이터를 나타내는지 출력하는 함수
def draw_fruits(arr):
n = len(arr) # 샘플 수
# 한 줄에 10개씩 이미지를 그릴 때, 몇 개 행이 필요할지 행 개수 계산
rows = int(np.ceil(n / 10))
cols = 10
fig, axs = plt.subplots(rows, cols, figsize = (cols, rows), squeeze = False)
for i in range(rows):
for j in range(cols):
if i * 10 + j < n:
axs[i, j].imshow(arr[i * 10 + j], cmap = "gray_r")
axs[i, j].axis("off")
plt.show()
draw_fruits(fruits[km.labels_ == 0])

draw_fruits(fruits[km.labels_ == 1])

draw_fruits(fruits[km.labels_ == 2])

클러스터 중심
- KMeans 가 최종적으로 찾은 클러스터 중심은 cluster_centers_ 속성에 저장됨
- transform 메서드를 이용하면 입력데이터로부터 각 클러스터 중심까지의 거리를 계산할 수 있음
- predict 메서드는 가장 가까운 클러스터를 예측 클래스로 출력
- KMeans가 반복학습한 횟수는 n_iter_ 속성에 저장됨
km.cluster_centers_
array([[1.01111111, 1.01111111, 1.01111111, ..., 1. , 1. ,
1. ],
[1.10204082, 1.07142857, 1.10204082, ..., 1. , 1. ,
1. ],
[1. , 1. , 1. , ..., 1. , 1. ,
1. ]])km.cluster_centers_.shape
(3, 10000)
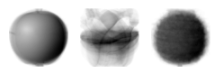
# 각 과일의 픽셀의 평균값을 출력한 것과 유사한 이미지
draw_fruits(km.cluster_centers_.reshape(-1, 100, 100))
km.transform(fruits_2d[[100]])
array([[5279.33763699, 8837.37750892, 3400.24197319]])
km.predict(fruits_2d[[100]])
array([2])
draw_fruits(fruits[[100]])

# 몇 바퀴 확인했는지 확인
km.n_iter_
4
최적의 k 찾기
- 현재 예제에서는 과일이 몇 종류 있는지 알고 있었기 때문에 클러스터의 개수를 3으로 지정
- 실전에서는 데이터를 몇 개의 클러스터로 나누어야할 지 알 수 없음
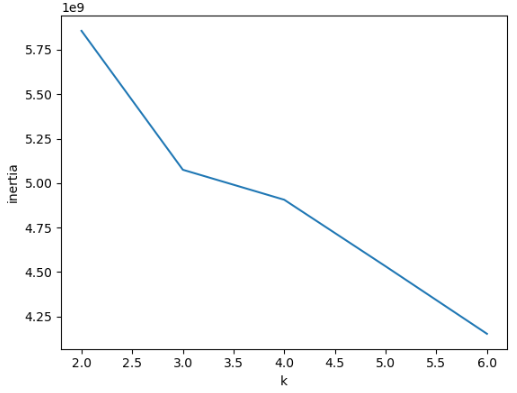
- elbow 기법
- 적절한 k값을 찾기 위한 대표적인 방법
- inertia(이너셔) : 각 샘플과 클러스터 중심 사이의 거리의 제곱 합
- 클러스터에 속한 샘플이 얼마나 가깝게 모여 있는지 나타내는 값
- 일반적으로 클러스터의 개수가 늘어나면 이너셔가 줄어듦
- elbow 기법은 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터를 찾는 방법
- 클러스터의 개수를 증가시키면서 이너셔를 그래프로 그리면 이너셔의 감소속도가 크게 변화하는 지점이 있음
- 이 지점 이후로는 클러스터 개수를 늘려도 이너셔가 크게 개선되지 않음
- 팔꿈치처럼 생긴 변곡점이 최적의 클러스터 개수
# 최적의 k를 찾는 방법
# 1. 도메인 지식 활용
# 2. elvow기법(가장 많이 사용)
# 3. silhouette(실루엣)계수
inertia = []
for k in range(2, 7):
km = KMeans(n_clusters = k, random_state = 26)
km.fit(fruits_2d)
inertia.append(km.inertia_)
plt.plot(range(2, 7), inertia)
plt.xlabel("k")
plt.ylabel("inertia")
plt.show()
728x90
'08_ML(Machine_Learning)' 카테고리의 다른 글
| 28_주 성분 분석 (0) | 2025.04.14 |
|---|---|
| 27_군집모델_심화 (2) | 2025.04.11 |
| 25_군집 알고리즘(비지도 학습)-과일 사진 레이블 없이 분류 (0) | 2025.04.11 |
| 24_파이프라인 구축 (0) | 2025.04.11 |
| 23_서포트 벡터 머신 (0) | 2025.04.11 |