728x90
데이터 전처리
01. 데이터 분할
- 머신러닝 모델의 성능을 정확하게 평가하기 위해서는 훈련에 사용하지 않은 테스트 세트를 통해 평가해야함
- 평가를 위한 별도의 데이터를 준비하거나 준비된 데이터 중에 일부를 떼어 테스트 세트로 준비
- 훈련: 테스트 비율은 70 ~ 80 : 20 ~ 30
- 반드시 정해져 있는 것은 아니며 연구자의 임의로 조절 가능함(예) 7:3, 75:25, 8:2)
- 전체 데이터가 아주 크고 모든 데이터 패턴을 잘 담아내기만 한다면 테스트 데이터는 1%만 사용해도 충분할 수 있음
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder, StandardScaler # 정규화
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split # 데이터 분할
df = pd.read_csv("./data/Fish.csv")
df = df.loc[df["Species"].isin(["Bream", "Smelt"]), ["Species", "Weight", "Length2"]]
le = LabelEncoder()
df["label"] = le.fit_transform(df["Species"])
df.head()
df.tail()

df.shape
(49, 4)
02. 샘플링 편향
- 훈련 세트에 도미 데이터와 빙어 데이터가 골고루 들어가 있지 않다면 올바르게 분류할 수 없음
- 예) 빙어 없이 모델 훈련이 이루어진다면 어떤 데이터를 빙어로 분류해야할지 알 수 없음
- 데이터가 골고루 섞여있지 않으면 샘플링이 한쪽으로 치우쳤다는 의미로 샘플링 편향(sampling bias)라고 부름
train_test_split()
- 전달되는 리스트나 배열을 섞은 후 비율에 맞게 훈련 세트와 테스트 세트로 나누어 주는 함수
- 매개변수
- 첫 번째 매개변수: 피처 데이터 세트(독립변수)
- 두 번째 매개변수: 레이블 데이터 세트(종속변수)
- test_size
- 전체 데이터에서 테스트 세트 크기를 얼마로 샘플링 할 것인가를 결정
- 초기값은 0.25
- train_size
- 전체 데이터에서 학습용 데이터 세트 크기를 얼마로 샘플링 할 것인가를 결정
- 일반적으로는 test_size를 활용
- test_size를 결정하면 자동으로 결정됨
- shuffle
- 데이터를 분리하기 전에 데이터를 미리 섞을지를 결정
- 초기값은 True
- 데이터를 분산시켜서 좀 더 효율적인 학습 및 테스트 데이터 세트를 만드는 데 사용
- random_state
- 매번 코드를 실행할 때마다 다른 결과가 나온다면 정확하게 모델을 평가할 수 없고 모델 최적화에 어려움이 있음
- 난수를 생성할 때 특정한 규칙으로 생성해서 매번 같은 결과가 나오게 통제할 수 있음
- stratify
- 무작위로 데이터를 섞으면 샘플링 편향이 일어날 수 있기 때문에 기존 데이터의 비율과 같은 비율로 데이터를 나눌 수 있도록 할 수 있음
- 반환값
- 튜플 형태
- 훈련 데이터의 피처, 테스트 데이터의 피처, 훈련 데이터의 레이블, 테스트 데이터의 레이블 이 순서대로 반환
x_train, x_test, y_train, y_test = train_test_split(df[["Length2", "Weight"]],
df["label"],
test_size = 0.25,
stratify = df["label"], # 빙어의 비율을 일정하게
random_state = 23 #실행할 때마다 결과가 달라지면 안되므로 설정(값은 자유)
)
print(len(x_train), len(x_test), len(y_train), len(y_test))
36 13 36 13
y_test
155 1
27 0
157 1
31 0
25 0
7 0
148 1
9 0
19 0
13 0
12 0
151 1
26 0
Name: label, dtype: int32
plt.figure()
plt.scatter(x_train["Length2"], x_train["Weight"], label = "train")
plt.scatter(x_test["Length2"], x_test["Weight"], label = "test")
plt.legend()
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
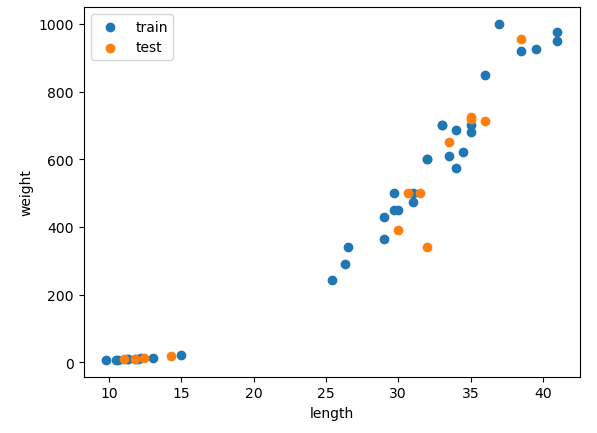
02. 모델 훈련
knn = KNeighborsClassifier()
knn.fit(x_train, y_train)
03. 모델 평가
knn.score(x_test, y_test)
1.0
04. 모델 최적화
plt.figure()
plt.scatter(x_train.iloc[:, 0], x_train.iloc[:, 1])
plt.scatter(25, 150, marker = "^")
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
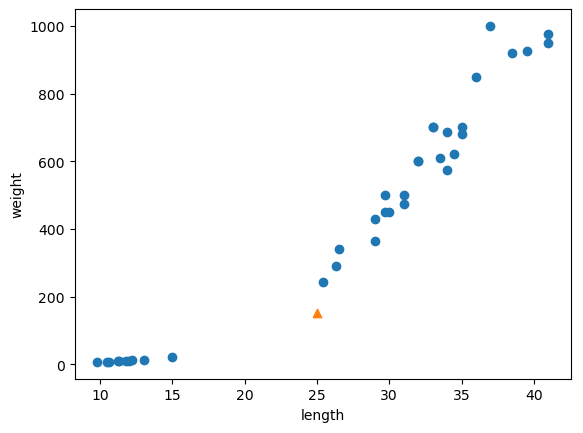
# 길이 25, 무게 150의 생선에 대한 예측
knn.predict([[25, 150]])
array([1])
le.inverse_transform([1])
array(['Smelt'], dtype=object)
- kneighbors()
- 이웃까지의 거리와 이웃 샘플의 인덱스를 반환
dist, idx = knn.kneighbors([[25, 150]])
x_train.iloc[idx.flatten()] # k값의 default=5
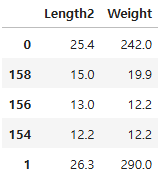
y_train.iloc[idx.flatten()]
0 0
158 1
156 1
154 1
1 0
Name: label, dtype: int32
plt.figure()
plt.scatter(x_train.iloc[:, 0], x_train.iloc[:, 1])
plt.scatter(25, 150, marker = "^")
plt.scatter(x_train.iloc[idx.flatten(), 0], x_train.iloc[idx.flatten(), 1], marker = "D")
plt.xlabel("length")
plt.ylabel("weight")
plt.show()

dist
array([[ 92.00086956, 130.48375378, 138.32150953, 138.39320793,
140.00603558]])- x축은 범위가 좁고, y축은 범위가 넓기 때문에 y축으로 조금만 벌어져도 큰 값으로 거리가 계산됨
plt.figure()
plt.scatter(x_train.iloc[:, 0], x_train.iloc[:, 1])
plt.scatter(25, 150, marker = "^")
plt.scatter(x_train.iloc[idx.flatten(), 0], x_train.iloc[idx.flatten(), 1], marker = "D")
plt.xlim(0, 1000)
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
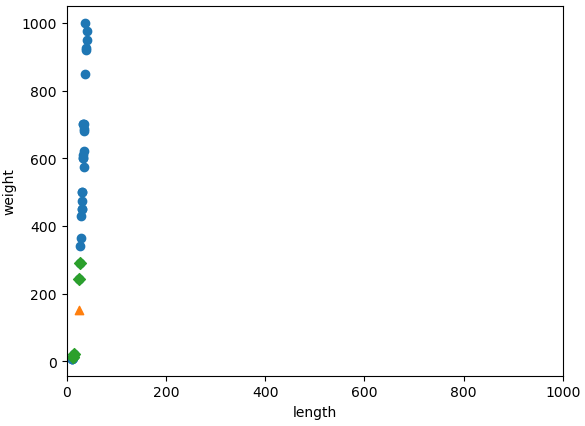
- 시각화 자료를 참고하면 현재 데이터에서 생선의 길이는 모델이 값을 예측하는 데에 거의 사용되지 않고 있음
- 두 독립변수의 단위가 다르기 때문에
- knn은 특히 데이터 간 거리가 모델 성능에 영향을 많이 주는 특성이 있음
- 각 독립변수의 단위가 다르면 올바른 예측이 어려울 가능성이 높음
- 각 독립변수의 단위를 일정한 기준으로 맞춰 주는 작업을 스케일링(scaling)이라고 함
05. 스케일링
- 스탠다드 스케일링(standard scaling)
- 각 피처값이 평균에서 표준편차의 몇 배만큼 떨어져있는지를 나타내 데이터의 단위와 관계없이 동일한 조건으로 비교할 수 있게 변환
- 분산: 데이터에서 평균을 뺀 값을 모두 제곱한 다음 평균을 계산
- 표준편차: 분산의 제곱근. 데이터가 분산된 정도
- 평균이 0이고 분산이 1인 가우시안 정규 분포를 가진 값으로 변환
- 몇몇 알고리즘에서는 데이터가 가우시안 정규 분포를 가지고 있다고 가정하고 구현하기 때문에 스탠다드 스케일링이 예측 성능 향상에 중요한 요소가 될 수 있음
- 예) 서포트 벡터 머신, 선형 회귀, 로지스틱 회귀
- 몇몇 알고리즘에서는 데이터가 가우시안 정규 분포를 가지고 있다고 가정하고 구현하기 때문에 스탠다드 스케일링이 예측 성능 향상에 중요한 요소가 될 수 있음
- 계산식
- (특성값 - 평균) / 표준편차
- 각 피처값이 평균에서 표준편차의 몇 배만큼 떨어져있는지를 나타내 데이터의 단위와 관계없이 동일한 조건으로 비교할 수 있게 변환
- MinMaxScaler
- 데이터 값을 0과 1사이의 범위 값으로 변환
- 음수 값이 있으면 -1에서 1사이의 값으로 변환
- 데이터 값을 0과 1사이의 범위 값으로 변환
- 학습 데이터와 테스트 데이터의 스케일링 변환 시 유의점
- scaler 객체를 이용해 데이터 스케일링 변환 시 사용 메서드
- fit()
- 데이터 변환을 위한 기준 정보 설정
- 예) 데이터 세트의 최댓값/최솟값 설정 등
- transform()
- fit()으로 설정된 정보를 이용해 데이터를 변환
- fit_transform()
- fit()과 transform()을 한 번에 적용
- fit()
- 학습 데이터로 fit()이 적용된 스케일링 기준 정보를 그대로 테스트 데이터에 적용해야함
- 테스트 데이터로 다시 새로운 스케일링 기준 정보를 만들게 되면 학습 데이터와 테스트 데이터의 스케일링 기준 정보가 서로 달라지기 때문에 올바른 예측 결과를 도출하지 못함
- scaler 객체를 이용해 데이터 스케일링 변환 시 사용 메서드
# 스탠다드 스케일링 객체 생성
ss = StandardScaler()
scaled_x_train = ss.fit_transform(x_train)
scaled_x_train
array([[-0.05462992, -0.33822937],
[ 0.78120782, 0.75936249],
[ 0.63370704, 0.48496453],
[-0.07429669, -0.49067268],
[ 0.87954167, 1.21669243],
[ 1.22371015, 1.4453574 ],
[-1.50013753, -1.34466012],
[ 1.37121092, 1.59780071],
[ 0.26003841, 0.14958924],
[ 0.48620626, 0.45447586],
[-1.48047076, -1.34496501],
[ 0.38787241, 0.07336758],
[ 0.97787552, 1.67402237],
[ 0.48620626, 0.45447586],
[-0.16279715, -0.63701826],
[-1.46080399, -1.33764773],
[ 0.28953856, -0.00285408],
[ 0.19120471, -0.26810544],
[ 0.78120782, 0.69838516],
[ 0.26003841, -0.00285408],
[-1.62797153, -1.3519774 ],
[-1.69680523, -1.35441649],
[ 0.73204089, 0.51545319],
[ 0.38787241, 0.14958924],
[ 1.37121092, 1.52157906],
[-1.55913784, -1.34496501],
[-1.3821369 , -1.33764773],
[ 0.68287396, 0.37825421],
[-1.61813815, -1.35350184],
[ 0.19120471, -0.0638314 ],
[ 0.58454011, 0.75936249],
[ 0.58454011, 0.75936249],
[ 0.68287396, 0.7136295 ],
[-1.1854692 , -1.31417146],
[-1.54930445, -1.34831876],
[ 1.12537629, 1.43011307]])
# 스케일링된 데이터 시각화
plt.figure()
plt.scatter(scaled_x_train[:, 0], scaled_x_train[:, 1])
plt.scatter(25, 150, marker = "^")
plt.ylabel("length")
plt.ylabel("weight")
plt.show()
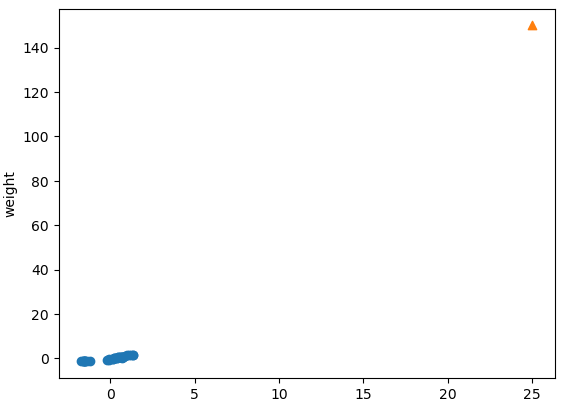
- 값의 스케일이 달라졌기 때문에 테스트 데이터도 스케일링 해줘야 함
scaled_data = ss.transform([[25, 150]])
scaled_data
array([[-0.20213069, -0.91751396]])
plt.figure()
plt.scatter(scaled_x_train[:, 0], scaled_x_train[:, 1])
plt.scatter(scaled_data[0, 0], scaled_data[0, 1], marker = "^")
plt.ylabel("length")
plt.ylabel("weight")
plt.show()
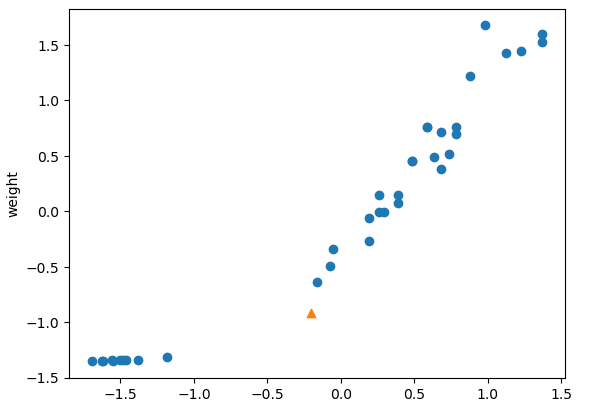
# 테스트 데이터 스케일링
scaled_x_test = ss.transform(x_test)
# 스케일링된 데이터로 다시 모델 구현
knn = KNeighborsClassifier()
knn.fit(scaled_x_train, y_train)
knn.score(scaled_x_test, y_test)
1.0
# 문제의 데이터 예측
knn.predict(scaled_data)
array([0])
# 시각화
dist, idx = knn.kneighbors(scaled_data)
plt.figure()
plt.scatter(scaled_x_train[:, 0], scaled_x_train[:, 1])
plt.scatter(scaled_data[0, 0], scaled_data[0, 1], marker = "^")
plt.scatter(scaled_x_train[idx.flatten(), 0], scaled_x_train[idx.flatten(), 1], marker = "D")
plt.ylabel("length")
plt.ylabel("weight")
plt.show()

728x90
'08_ML(Machine_Learning)' 카테고리의 다른 글
| 06_KNN 심화 (0) | 2025.04.04 |
|---|---|
| 05_KNN회귀 (0) | 2025.04.04 |
| 04_KNN_타이타닉 분류 (0) | 2025.04.02 |
| 02_KNN 이진분류 (0) | 2025.04.02 |
| 01. 머신러닝 기본 이론 (2) | 2025.04.02 |