728x90
카이제곱 검정(Chi-square test)
- 범주형 변수들 간의 연관성을 분석하기 위해 결합분포를 활용하는 방법
- 연령 같은 변수는 연령대와 같은 서열척도로 변환해서 사용할 수 있음
- 기본 원리는 변수들 간의 범주를 동시에 교차하는 교차표를 만들어 각각의 빈도와 비율을 통해 변수 상호 간의 독립성과 관련성을 분석하는 것
- 교차분석은 상관분석과는 다르게 연관성의 정도를 수치로 표현할 수 없음
- 대신 검정 통계량 카이 제곱을 통해 변수 간에 연관성이 없다는 귀무가설을 기각하는지 여부로 상관성이 있고 없음을 판단
from scipy.stats import chi2_contingency
import pandas as pd
import matplotlib.pyplot as plt
df.head()
df.shape
(131, 2)
df.isna().sum()
sex 0
smoke 0
dtype: int64
# 항목별 집계
df.groupby(["sex", "smoke"]).size()
sex smoke
female Non-Smoker 50
Smoker 12
male Non-Smoker 40
Smoker 29
dtype: int64
- 남성과 여성의 흡연자와 비흡연자수 현황을 파악하기 위해 groupby() 함수로 집계 데이터를 산출
- 여성은 62명 중 12명이 흡연자고, 남성은 69명 중 29명이 흡연자임
# 카이제곱 검정용 데이터셋 가공
crosstab = pd.crosstab(df["sex"], df["smoke"]) # 교차표 생성
crosstab
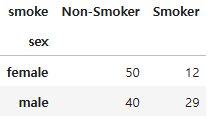
# 성별 별 흡연자 수 시각화
crosstab.plot(kind = "bar", figsize = (10, 5))
plt.grid()
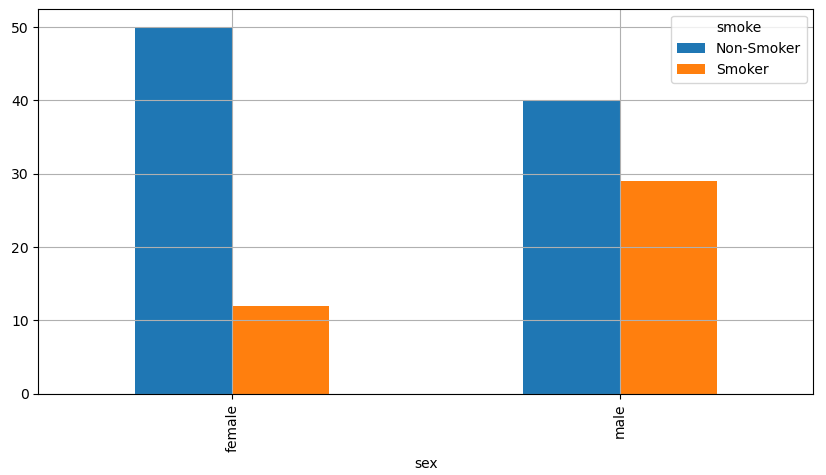
- 카이제곱 검정을 하기에 앞서 항목별 분포를 막대그래프로 시각화
- 눈으로 보기에도 남성과 여성의 흡연자 비율 차이가 크게 남
- 이러한 차이가 통계적으로 유의미한 차이인지 확인하기 위해 카이제곱 검정을 수행
# 카이제곱 검정
chiresult = chi2_contingency(crosstab)
chiresult
Chi2ContingencyResult(statistic=6.789242038107618, pvalue=0.009170883871905303, dof=1, expected_freq=array([[42.59541985, 19.40458015],
[47.40458015, 21.59541985]]))
- p-value가 0.05보다 작게 나타나 성별에 따른 흡연자 비율 차이가 통계적으로 유의함
728x90
'07_Data_Analysis' 카테고리의 다른 글
| 17_유투브 랭킹 데이터 분석 (0) | 2025.03.19 |
|---|---|
| 16_기온 데이터 분석 (0) | 2025.03.19 |
| 14_ANOVA(ANalysis Of VAriance) (2) | 2025.03.19 |
| 13_T-Test (0) | 2025.03.19 |
| 12_T-Test, ANOVA 개요 (0) | 2025.03.19 |