728x90
ANOVA(ANalysis Of VAriance)
- T-test는 두 집단의 평균 차이를 검정하는 방법
- 세 집단 이상의 평균을 검정할 때는 ANOVA를 사용
- T-test를 사용하여 세 집단 이상을 분석할 때는 A와 B를 검정하고, B와 C를 검정하고, A와 C를 검정하는 방법을 사용
- 하지만 신뢰도가 하락하는 문제가 있어 일반적으로 집단이 3개 이상일 때는 ANOVA를 사용
- ANOVA의 일반적인 가설
- H0(귀무가설) : 독립변수의 차이에 따른 종속변수는 동일하다
- H1(대립가설) : 독립변수의 차이에 따른 종속변수는 다르다
- ANOVA는 독립변수의 수에 따라 다르게 불림
- 예) 고객들의 객단가 평균 차이를 비교하기 위한 요인이 '지역' 하나라면 일원 분산분석(one-way ANOVA)
- 만약 요인이 '지역', '연령대' 두 가지라면 이원 분산분석(two-way ANOVA), 더 많은 N가지라면 N원 분산분석(N-way ANOVA)라고 함
- ANOVA를 사용할 때, 독립변수는 집단을 나타낼 수 있는 범주형 변수여야 하며, 종속변수는 연속형 변수여야 함
- 독립변수와 종속변수가 연속형일 때는 회귀분석
- 독립변수와 종속변수가 범주형일 때는 교차분석을 사용함
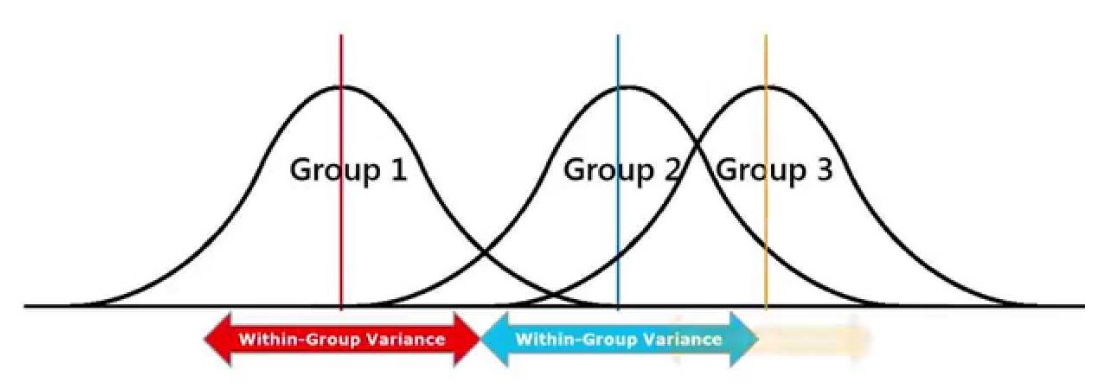
- ANOVA는 각 집단의 평균이 서로 멀리 떨어져 있어 집단 평균의 분산이 큰 정도를 따져서 집단 간 평균이 다른지 판별
- 집단 내 각 관측치들이 집단 평균으로부터 얼마나 퍼져 있는지를 나타내는 집단 내 분산
- 전체 집단의 통합 평균과 각 집단의 평균값이 얼마나 퍼져 있는지를 나타내는 집단 간 분산이 사용됨
- 예) 위 이미지에서 집단2와 집단3 처럼 집단간의 겹치는 부분이 큰 경우는 각 집단의 평균이 다르다고 보기 어려움
- 반면에 집단1의 평균은 멀리 떨어져 있어 집단 간 평균 차이가 확실히 난다고 볼 수 있음
- 집단 간 평균의 분산을 집단 내 분산으로 나눈 값이 유의도 임계치를 초과하는지 여부에 따라 집단 간 평균의 차이를 검정
- ANOVA 분석의 결과만으로는 각 집단의 평균이 모두 다른 것인지, 일부만 다른 것인지는 알 수 없음
- 일부 집단들은 집단간 차이가 없을 수 있음
- 이러한 1종 오류(귀무가설이 참임에도 불구하고 귀무가설을 기각하는 오류)를 방지하기 위해 사후 검증을 수행 ※1종 오류: 귀무가설O -> 대립가설 채택 오류 2종 오류: 귀무가설x -> 귀무가설 채택 오류
- 사후 검증은 집단 크기가 같을 때 사용하는 Tukey의 HSD검증, 집단의 크기가 다를 때 사용하는 scheffe 검증 방법 등이 있음
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from statsmodels.stats.multicomp import pairwise_tukeyhsd
from scipy import stats
import pandas as pd
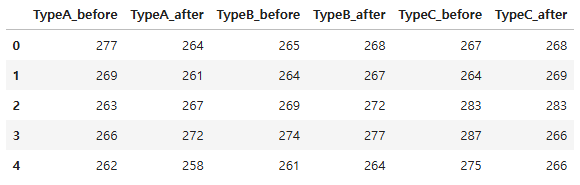
df = pd.read_csv("./data/Golf_test.csv")
df.head()
# scipy 패키지 아노마 검정
F_statistic, p_value = stats.f_oneway(df["TypeA_before"],
df["TypeB_before"],
df["TypeC_before"])
print(f"일원분산분석 결과 : F = {F_statistic:.1f}, p = {p_value:.5f}")
일원분산분석 결과 : F = 4.2, p = 0.01652
- 정규성 검정과 등분산성 검정은 T-test에서 수행했으므로 생략
- pvalue가 0.05보다 작으므로, 3개의 집단 중 최소한 하나의 집단은 통계적으로 유의미한 차이가 있음
# statsmodels 패키지 사용을 위해 데이터 재구조화
df2 = pd.melt(df)
df2.head()
df2 = df2[df2["variable"].isin(["TypeA_before", "TypeB_before", "TypeC_before"])]
df2.shape
(150, 2)
df2[df2["variable"].str.endswith("_before")].shape
(150, 2)
- statsmodels 패키지 사용을 위한 전처리
- 각 골프공 조건이 개별 컬럼으로 구성되어 있기 때문에 variable 컬럼과 value컬럼으로 재구조화
# statsmodels 아노바 검정
model = ols("value ~ C(variable)", df2).fit() # R문법: 종속변수 ~ 독립변수
anova_lm(model)
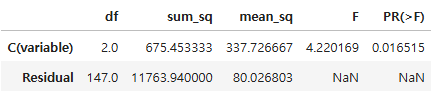
- 앞서 수행한 ANOVA 검정과 동일한 결과
- 데이터셋의 형태에 따라 사용하기 편한 패키지를 선택하면 됨
df2["variable"].value_counts()
variable
TypeA_before 50
TypeB_before 50
TypeC_before 50
Name: count, dtype: int64# 사후검정
posthoc = pairwise_tukeyhsd(df2["value"],
df2["variable"],
alpha = 0.05) # alpha: 유의수준 default=0.05
print(posthoc)
Multiple Comparison of Means - Tukey HSD, FWER=0.05
===============================================================
group1 group2 meandiff p-adj lower upper reject
---------------------------------------------------------------
TypeA_before TypeB_before 5.14 0.0129 0.9038 9.3762 True
TypeA_before TypeC_before 1.9 0.5392 -2.3362 6.1362 False
TypeB_before TypeC_before -3.24 0.1696 -7.4762 0.9962 False
---------------------------------------------------------------fig = posthoc.plot_simultaneous()
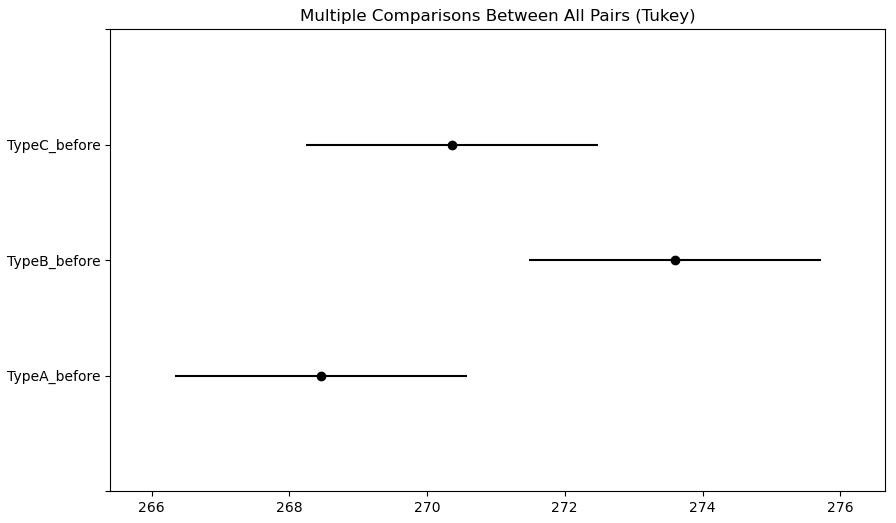
- Tukey 의 HSD 사후 검정을 수행
- TypeA_before와 TypeB_before 간에만 유의미한 차이가 있고, 나머지 조합에서는 통계적으로 유의미한 차이가 없음
728x90
'07_Data_Analysis' 카테고리의 다른 글
| 16_기온 데이터 분석 (0) | 2025.03.19 |
|---|---|
| 15_카이제곱 검정(교차분석) (0) | 2025.03.19 |
| 13_T-Test (0) | 2025.03.19 |
| 12_T-Test, ANOVA 개요 (0) | 2025.03.19 |
| 11_탐색적 데이터 분석_국가별 음주 데이터 분석 (1) | 2025.03.19 |