728x90
의사 결정 나무
모델의 직관성과 가시성을 높여 모델 설명력을 높이기 위해 사용
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier, plot_tree, export_text
df = pd.read_csv("./data/wine.csv")
df.head()
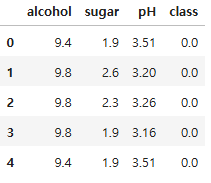
- alcohol: 알코올 도수
- sugar: 당도
- pH: pH값
- class: 타깃 값. 0이면 레드와인, 1이면 화이트 와인
df.shape
(6497, 4)
df.dtypes
alcohol float64
sugar float64
pH float64
class float64
dtype: object
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 6497 entries, 0 to 6496
Data columns (total 4 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 alcohol 6497 non-null float64
1 sugar 6497 non-null float64
2 pH 6497 non-null float64
3 class 6497 non-null float64
dtypes: float64(4)
memory usage: 203.2 KB
df.describe()
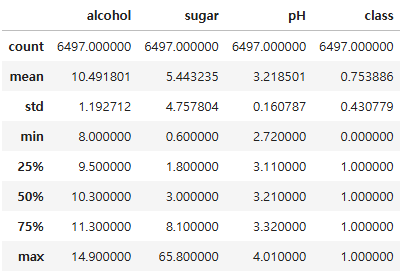
x = df.drop("class", axis = 1)
y = df["class"]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, stratify = y, random_state = 26)
x_train.shape, x_test.shape
((5197, 3), (1300, 3))
ss = StandardScaler()
scaled_train = ss.fit_transform(x_train)
scaled_test = ss.transform(x_test)
logi = LogisticRegression()
logi.fit(scaled_train, y_train)
print(logi.score(scaled_train, y_train))
print(logi.score(scaled_test, y_test))
0.7819896093900327
0.7807692307692308
logi.coef_, logi.intercept_
(array([[ 0.54435293, 1.61800398, -0.7194883 ]]), array([1.76898932]))# alc sugar pH
- 로지스틱 회귀 모델은 이해하기 어려움
- 왜 저런 계수값이 나왔는지 이해하기 어려움
- 알코올 도수와 당도가 높을 수록, pH가 낮을 수록 화이트와인일 가능성이 높음
- 만약에 다항특성과 하이퍼파라미터 튜닝이 추가되면 더 설명하기 어려운 모델이 됨
의사 결정 나무
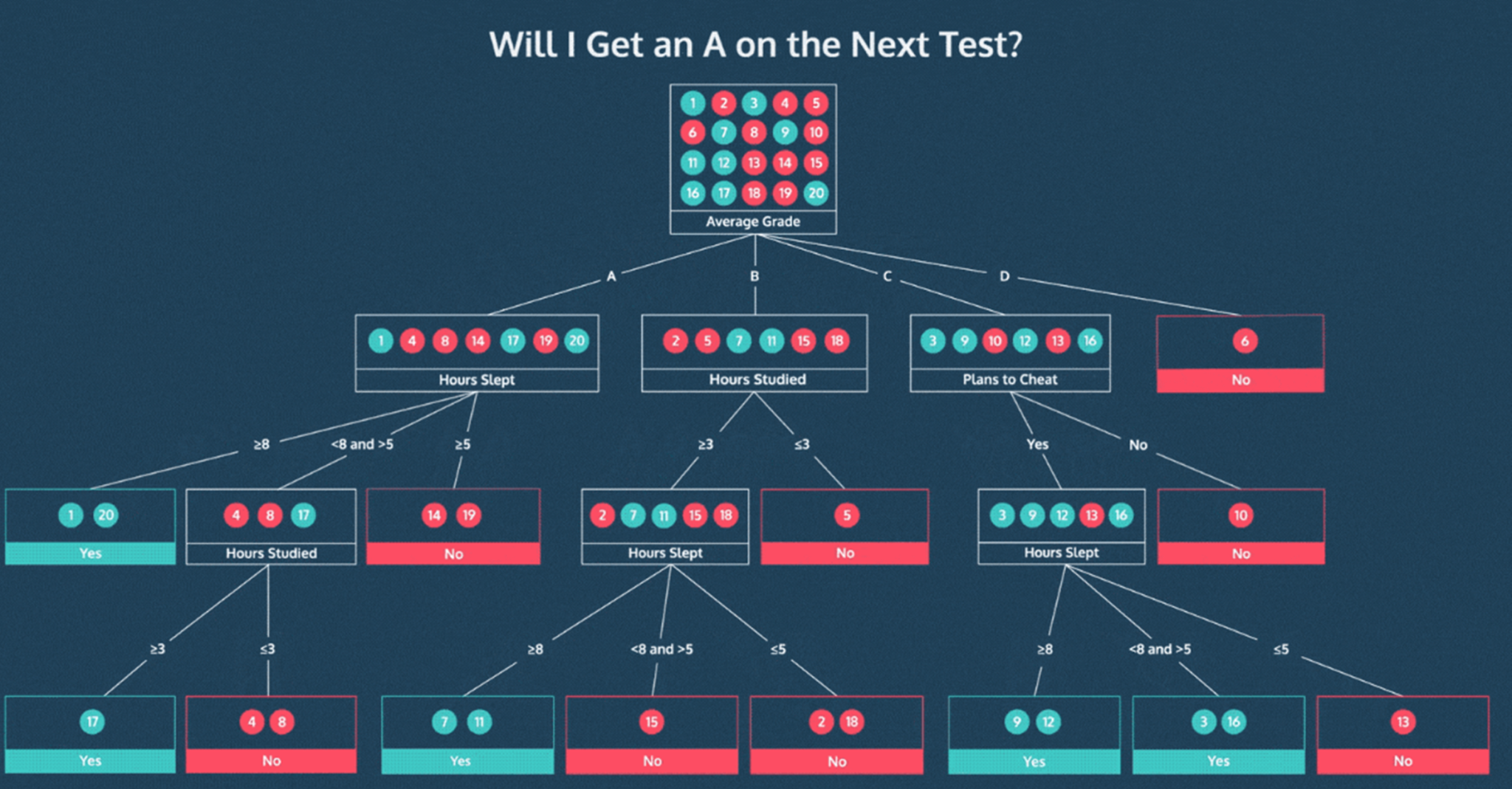
- 의의
- 한 번에 하나씩의 독립변수를 사용하여 예측 가능한 규칙들의 집합을 생성하는 알고리즘
- 질문을 던져서 대상을 좁혀나가는 스무고개와 비슷한 개념
- 분류와 회귀 모두 가능함
- 범주형 데이터, 연속형 데이터 모두 예측 가능
- 장점
- 다른 지도학습 기법들에 비해 해석이 쉬움
- 유용한 독립변수를 파악할 수 있음
- 선형성, 정규성, 등분산성 등의 수학적 가정이 불필요한 비모수적 모형임
- 스케일링을 할 필요가 없음
- 스케일링이 의사결정나무 알고리즘에 아무런 영향을 주지 않음(결과가 같으므로)
- 단점
- 성능이 떨어지는 경우가 많음
- 분류 기준값의 경계선 주변의 자료에서는 오차가 클 수 있음
- 각 예측 변수의 효과를 파악하기 어려움
- 예측이 불안정할 수 있음
dt = DecisionTreeClassifier(random_state = 26)
# 학습
dt.fit(scaled_train, y_train)
print(dt.score(scaled_train, y_train))
print(dt.score(scaled_test, y_test))
0.9974985568597268
0.8630769230769231
시각화
plt.figure()
plot_tree(dt)
plt.show()
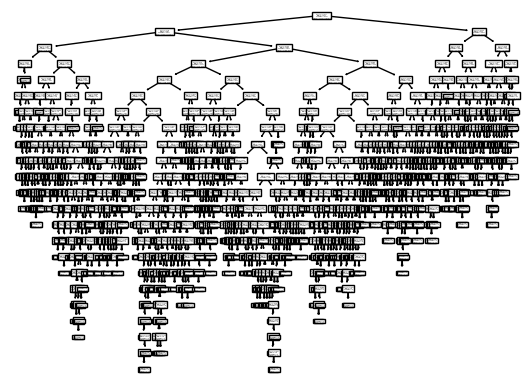
- 모델이 너무 복잡하기 때문에 트리의 깊이를 제한해서 출력할 필요가 있음
- max_depth: 루트 노드를 제외하고 더 확장하여 그릴 깊이
- filled: 클래스에 맞게 색을 칠함
- feature_names: 특성의 이름을 전달
plt.figure(figsize = (10, 7))
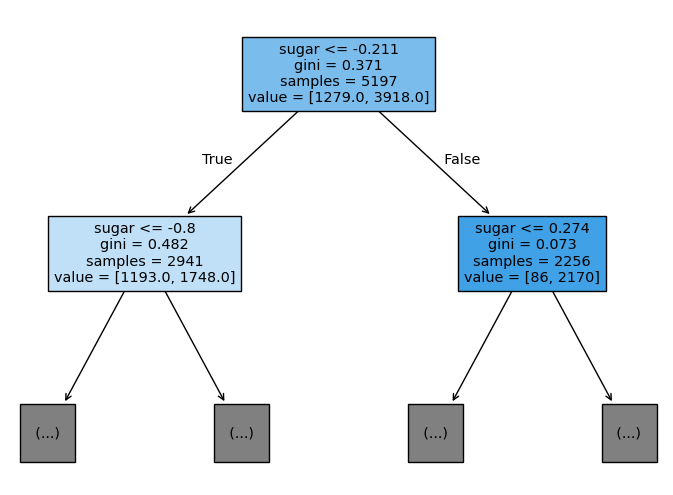
plot_tree(dt, max_depth = 1, filled = True, feature_names = ["alcohol", "sugar", "pH"])
plt.show()
# 분류 규칙 텍스트 출력
print(export_text(dt, feature_names = ["alcohol", "sugar", "pH"]))
|--- sugar <= -0.21
| |--- sugar <= -0.80
| | |--- sugar <= -0.85
| | | |--- pH <= 4.21
| | | | |--- sugar <= -0.89
| | | | | |--- pH <= -2.03
| | | | | | |--- pH <= -2.09
| | | | | | | |--- class: 1.0
| | | | | | |--- pH > -2.09
| | | | | | | |--- class: 0.0
| | | | | |--- pH > -2.03
| | | | | | |--- class: 1.0
| | | | |--- sugar > -0.89
| | | | | |--- alcohol <= -0.54
| | | | | | |--- alcohol <= -0.62
| | | | | | | |--- pH <= -0.33
...
dt.tree_.feature
array([ 1, 1, 1, ..., -2, -2, -2], dtype=int64)
dt.tree_.threshold
array([-0.21050891, -0.79994234, -0.85257035, ..., -2. ,
-2. , -2. ])
dt.tree_.node_count
1547
시각화 해석 방법
- 맨 위의 노드를 root note(루트 노드), 맨 아래의 노드를 leaf node(리프 노드)라고 함
- 루트 노드는 sugar가 -0.211 이하인지 질문
- 각 데이터 샘플의 sugar가 -0.211 이하이면 왼쪽 가지로 이동
- 그렇지 않으면 오른쪽 가지로 이동
- 루트 노드의 총 샘플 수는 5197개
- 이 중에서 음성 클래스(레드 와인)은 1279개
- 양성 클래스(화이트와인)는 3918개
- 왼쪽 노드는 sugar가 -0.8이하인지 질문
- yes는 왼쪽 가지, no는 오른쪽 가지로 이동
- 노드의 총 샘플 수는 2941개
- 음성 클래스와 양성 클래스 개수는 각각 1193, 1748개
- 오른쪽 노드는 sugar가 0.274이하인지 질문
- 노드의 총 샘플 수는 2256개
- 음성 클래스와 양성 클래스 개수는 각각 86, 2170개
- 노드의 총 샘플 수는 2256개
- 왼쪽 노드는 색깔이 더 연해지고 오른쪽 노드는 더 진해짐
- 양성 클래스의 비율이 높아질 수록 진한 색으로 표시됨
- 예측 방법은 리프노드에서 가장 많은 클래스가 예측 클래스가 됨
- 만약에 이 단계에서 성장을 멈춘다면 왼쪽 노드에 도달한 샘플과 오른쪽 노드에 도달한 샘플 모두 양성 클래스로 예측됨
- 불순도(여러가지 데이터들이 섞여있으면 불순)
- Gini impurity(지니 불순도)
- DecisionTreeClassifier의 criterion매개변수의 기본값이 gini
- criterion
- 노드에서 데이터를 분할할 기준
- 지니 불순도 계산식
- 지니 불순도 = 1 - (음성 클래스 비율^2 + 양성 클래스 비율^2)
- 예) 1- ((1279 / 5197)^2 + (3918 / 5197)^2) = 0.371
- 지니 불순도 = 1 - (음성 클래스 비율^2 + 양성 클래스 비율^2)
1- ((1279 / 5197)**2 + (3918 / 5197)**2)
0.37107315616915937
# 순수 노드 지니 불순도
1 - ((0 / 100)**2 + (100 / 100)**2)
0.0
# 최악의 지니 불순도
1 - ((50 / 100)**2 + (50 / 100)**2)
0.5
- 따라서 의사결정나무 모델은 parent node(부모 노드)와 child node(자식 노드)의 불순도 차이가 가능한 크도록 트리를 성장시킴
- 불순도의 차이
- 부모의 불순도 - (왼쪽 노드 샘플 수 / 부모의 샘플 수) * 왼쪽 노드 불순도 - (오른쪽 노드 샘플 수 / 부모의 샘플 수) * 오른쪽 노드 불순도
- 불순도의 차이
0.371 - (2941 / 5197) * 0.482 - (2256 / 5197) * 0.073
0.06654550702328269
- 이런 부모 노드와 자식 노드 사이의 불순도 차이를 information gain(정보 이득)이라고 부름
- 의사 결정 나무 알고리즘은 정보 이득이 최대가 되도록 데이터를 나눔
- 이 때 사용하는 기준이 지니 불순도
- 사이킷런에서 제공하는 또 다른 불순도 기준으로는 엔트로피 불순도가 있음
- 즉, 노드를 순수하게 나눌수록 정보 이득이 커짐
- 의사 결정 나무 알고리즘은 정보 이득이 최대가 되도록 데이터를 나눔
가지치기
- 깊이에 제한을 두지 않고 무작정 끝까지 자라나는 트리를 만들게 되면 훈련 세트에는 아주 잘 맞지만 테스트세트에는 적합하지 않은 과대적합 모델이 되어 일반화가 잘 되지 않음
- 트리의 성장을 제한하는 방법이 가지치기
- 가장 간단한 가지치기 방법은 트리의 최대 깊이를 지정하는 것
dt = DecisionTreeClassifier(max_depth = 3, random_state = 26)
dt.fit(scaled_train, y_train)
print(dt.score(scaled_train, y_train))
print(dt.score(scaled_test, y_test))
0.8454877814123533
0.8369230769230769
plt.figure(figsize = (20, 15))
plot_tree(dt, filled = True, feature_names = ["alcohol", "sugar", "pH"])
plt.show()
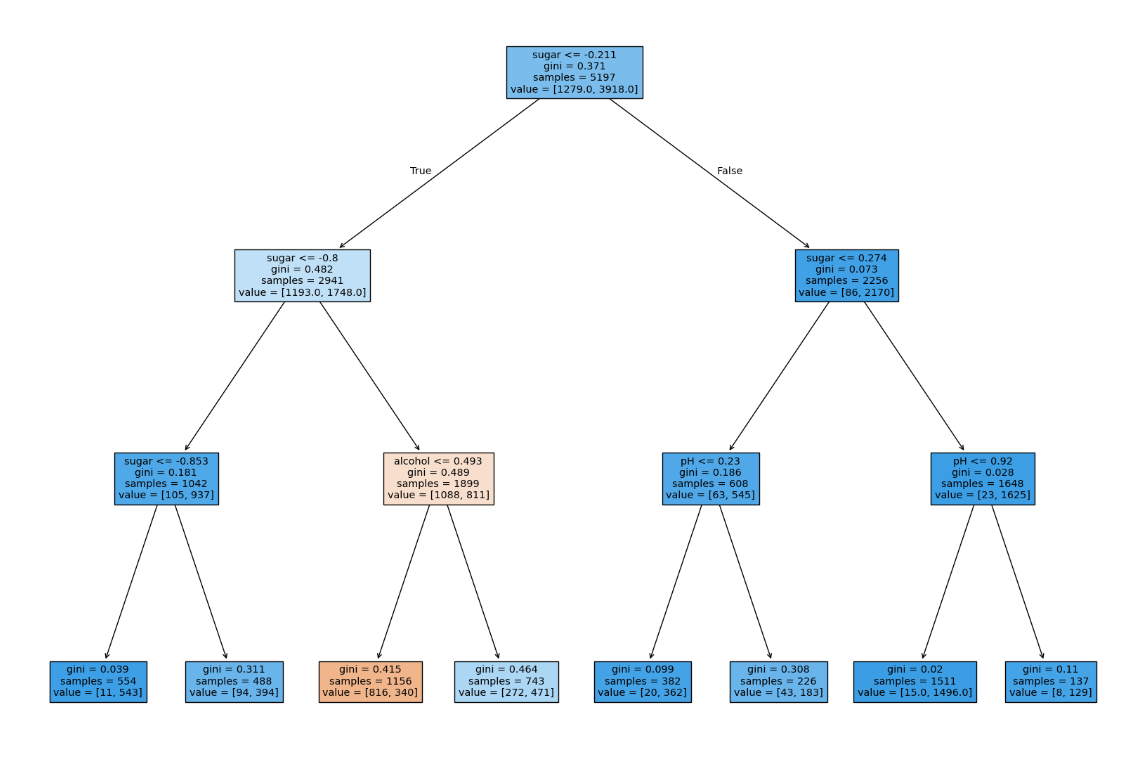
# 스케일링을 적용하지 않은 의사결정 나무(스케일링 적용된 데이터와 결과가 같다)
dt = DecisionTreeClassifier(max_depth = 3, random_state = 26)
dt.fit(x_train, y_train)
print(dt.score(x_train, y_train))
print(dt.score(x_test, y_test))
0.8454877814123533
0.8369230769230769
# 특성중요도
print(dt.feature_importances_)
[0.13425818 0.8580405 0.00770132]
- 특성 중요도
- 어떤 특성이 가장 유용한지 나타내는 지표
- 두 번째 특성인 sugar가 0.85로 가장 높음. alcohol, pH 순서
- 각 노드의 정보 이득과 전체 샘플에 대한 비율을 곱한 후 특성별로 더하여 계산
- 특성 중요도를 활용하여 변수 선택에 활용할 수 있음
728x90
'08_ML(Machine_Learning)' 카테고리의 다른 글
| 21_트리 앙상블 (0) | 2025.04.10 |
|---|---|
| 20_교차검증_그리드서치 (0) | 2025.04.10 |
| 18_확률적 경사 하강법 (0) | 2025.04.09 |
| 16_로지스틱 회귀분석_심화 (1) | 2025.04.08 |
| 15_로지스틱 감성분류(자연어 처리) - 맛집 리뷰 (6) | 2025.04.08 |