728x90
로지스틱 회귀분석(Logistic Regression)
- 선형 회귀분석과 유사하지만 종속변수가 양적 척도가 아닌 질적 척도임
- 특성 수치를 예측하는 것이 아니라 어떤 카테고리에 들어갈지 분류하는 모델
- 기본 모형은 종속변수가 0과 1이라는 이항(binary)으로 이루어져 구매/미구매, 성공/실패, 합격/불합격 등을 예측
- 만약 종속변수의 범주가 3개 이상일 경우에는 다항 로지스틱 회귀분석(Multinomial Logistic Regression)을 통해 분류 예측을 할 수 있음
- 로지스틱 회귀는 기존의 선형회귀식의 사상은 그대로 유지하되 종속변수를 1이 될 확률로 변환하여 그 확률에 따라 0과 1의 여부를 예측
- 선형 회귀선은 이항으로 이루어진 종속변수를 직선으로 표현하여 확률이 양과 음의 무한대로 뻗어나가게 됨
- 이러한 방식은 확률을 표현하기에 적합하지 않기 때문에 0과 1사이의 S자 곡선의 형태를 갖도록 변환해줘야 함
- 선형회귀선을 로짓회귀선으로 변환하기 위해서는 오즈값을 구해야 함
- 오즈(Odds): 사건이 발생할 가능성이 발생하지 않을 가능성보다 어느 정도 큰지를 나타내는 값
- 분모는 사건이 발생하지 않을 확률, 분자는 사건이 발생할 확률로 하여 사건이 발생하지 않을 확률 대비 사건이 발생할 확률을 비율로 나타냄
- 즉, 발생할 확률이 그렇지 않을 확률과 50 : 50으로 같으면 1.0, 두 배면 2.0, 다섯 배면 5.0 이됨
- 만약 발생확률이 60%이고 발생하지 않을 확률이 40%라면 발생확률이 1.5배 높기 때문에 오즈는 1.5가 됨

- 하지만 직선 형태의 회귀 값을 사건이 일어날 오즈값으로 변환하게 되면 발생확률이 1에 가까워질수록 기하급수적으로 커지고 최솟값은 0이 되는 균형잡히지 않은 형태가 됨
- 오즈(Odds): 사건이 발생할 가능성이 발생하지 않을 가능성보다 어느 정도 큰지를 나타내는 값

● 따라서 오즈 값에 로그를 취하면 양의 무한대에서 음의 무한대를 갖는 형태가 됨

하지만 여전히 0에서 1 사이의 범위를 나타내지 못하는 문제가 있음
- 따라서 확률을 로짓 변환하여 0에서 1사이로 치환
- 이 변환식을 시그모이드(Sigmoid) 함수라고 함

시그모이드 함수 적용 과정

- 이렇게 로지스틱 회귀분석은 사건 발생 확률을 0에서 1사이로 변환해서 표현
- 이러한 분류 모델은 카테고리를 분류하는 임계치를 어떻게 설정하는지가 중요
- 기본적으로 분류 기준값은 0.5
- 주제에 따라 달라질 수 있음
- 최적의 효율을 따져가며 분류 기준을 잡아야하기 때문에, 로지스틱 회귀 모델과 같은 분류 모델은 모델 성능 평가가 매우 중요
- 이러한 분류 모델은 카테고리를 분류하는 임계치를 어떻게 설정하는지가 중요
import pandas as pd
import numpy as np
from sklearn.preprocessing import RobustScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from imblearn.under_sampling import RandomUnderSampler
import statsmodels.api as sm
import seaborn as sns
import matplotlib.pyplot as plt
# 데이터 불러오기
df = pd.read_csv("./data/heart_2020_cleaned.csv")
df.head()

df.shape
(319795, 18)
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 319795 entries, 0 to 319794
Data columns (total 18 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 HeartDisease 319795 non-null object
1 BMI 319795 non-null float64
2 Smoking 319795 non-null object
3 AlcoholDrinking 319795 non-null object
4 Stroke 319795 non-null object
5 PhysicalHealth 319795 non-null float64
6 MentalHealth 319795 non-null float64
7 DiffWalking 319795 non-null object
8 Sex 319795 non-null object
9 AgeCategory 319795 non-null object
10 Race 319795 non-null object
11 Diabetic 319795 non-null object
12 PhysicalActivity 319795 non-null object
13 GenHealth 319795 non-null object
14 SleepTime 319795 non-null float64
15 Asthma 319795 non-null object
16 KidneyDisease 319795 non-null object
17 SkinCancer 319795 non-null object
dtypes: float64(4), object(14)
memory usage: 43.9+ MB
df.columns
Index(['HeartDisease', 'BMI', 'Smoking', 'AlcoholDrinking', 'Stroke',
'PhysicalHealth', 'MentalHealth', 'DiffWalking', 'Sex', 'AgeCategory',
'Race', 'Diabetic', 'PhysicalActivity', 'GenHealth', 'SleepTime',
'Asthma', 'KidneyDisease', 'SkinCancer'],
dtype='object')
# 명목형 변수 원핫인코딩(중간 과정 생략 가능)
df2 = pd.get_dummies(df, columns = ['HeartDisease', 'Smoking', 'AlcoholDrinking', 'Stroke',
'DiffWalking', 'Sex', 'AgeCategory', 'Race', 'Diabetic',
'PhysicalActivity', 'GenHealth', 'Asthma', 'KidneyDisease',
'SkinCancer'], drop_first = True)
# drop_first = True : 다중공선성을 피하기 위해 앞의 한 컬럼을 삭제
df2.head()
df2.columns
Index(['BMI', 'PhysicalHealth', 'MentalHealth', 'SleepTime',
'HeartDisease_Yes', 'Smoking_Yes', 'AlcoholDrinking_Yes', 'Stroke_Yes',
'DiffWalking_Yes', 'Sex_Male', 'AgeCategory_25-29', 'AgeCategory_30-34',
'AgeCategory_35-39', 'AgeCategory_40-44', 'AgeCategory_45-49',
'AgeCategory_50-54', 'AgeCategory_55-59', 'AgeCategory_60-64',
'AgeCategory_65-69', 'AgeCategory_70-74', 'AgeCategory_75-79',
'AgeCategory_80 or older', 'Race_Asian', 'Race_Black', 'Race_Hispanic',
'Race_Other', 'Race_White', 'Diabetic_No, borderline diabetes',
'Diabetic_Yes', 'Diabetic_Yes (during pregnancy)',
'PhysicalActivity_Yes', 'GenHealth_Fair', 'GenHealth_Good',
'GenHealth_Poor', 'GenHealth_Very good', 'Asthma_Yes',
'KidneyDisease_Yes', 'SkinCancer_Yes'],
dtype='object')
# 스케일링
# 숫자형 변수 분리
df_num = df2[['BMI', 'PhysicalHealth', 'MentalHealth', 'SleepTime']]
df_nom = df2.drop(['BMI', 'PhysicalHealth', 'MentalHealth', 'SleepTime'], axis = 1)
# nomical: 명목상의
# 숫자형 변수 RobustScaler 적용
rs = RobustScaler()
df_robust = rs.fit_transform(df_num)
● standard / minmax scaler는 이상치에 민감하게 반응
● robust scaler는 이상치의 영향 적음
df_num2 = pd.DataFrame(data = df_robust, columns = df_num.columns)
df_num.head()

df_num2.head()
# 숫자형 테이블과 더미화 문자형 테이블 결합
df3 = pd.concat([df_num2, df_nom], axis = 1)
df3.head()
# 독립변수와 종속변수 분리
x = df3.drop(["HeartDisease_Yes"], axis = 1)
y = df3[["HeartDisease_Yes"]]
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, stratify = y, random_state = 26)
x_train.shape, x_test.shape
((239846, 37), (79949, 37))
df3["HeartDisease_Yes"].value_counts()
HeartDisease_Yes
False 292422
True 27373
Name: count, dtype: int64
# HeartDisease_Yes 컬럼 클래스 분포 시각화
sns.countplot(data = y_train, x = "HeartDisease_Yes")
plt.show()
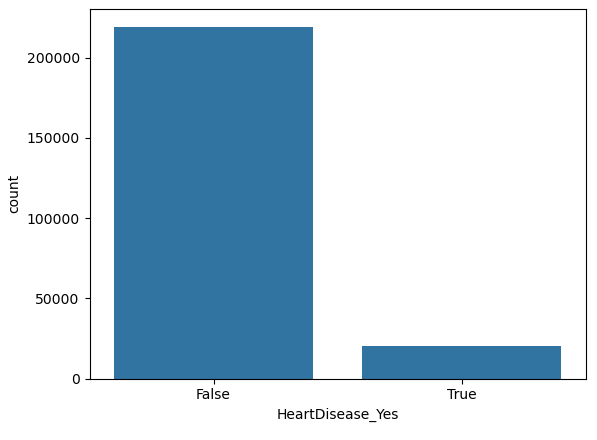
- 클래스 불균형이 심한 상황
- 언더 샘플링이나 오버 샘플링을 적용하여 클래스 균형을 맞춰 줘야 함
# 임시 변수명 적용
x_train_re = x_train.copy()
y_train_re = y_train.copy()
x_train.shape
(239846, 37)
x_temp_name = [f"X{i}" for i in range(1, 38)]
x_temp_name
['X1',
'X2',
'X3',
...
y_temp_name = ["y1"]
x_train_re.columns = x_temp_name
y_train_re.columns = y_temp_name
x_train_re.head()

- 기존 변수명은 언더샘플링이나 오버샘플링 적용시 오류가 발생하기 때문에 임시 변수명을 부여
# 언더샘플링 적용
x_train_under, y_train_under = RandomUnderSampler(random_state = 26).fit_resample(x_train_re, y_train_re)
print("언더샘플링 적용전")
print(x_train_re.shape, y_train_re.shape)
언더샘플링 적용전
(239846, 37) (239846, 1)
print("언더샘플링 적용후")
print(x_train_under.shape, y_train_under.shape)
언더샘플링 적용후
(41060, 37) (41060, 1)
print("언더샘플링 적용전 종속변수 분포")
print(y_train_re["y1"].value_counts())
언더샘플링 적용전 종속변수 분포
y1
False 219316
True 20530
Name: count, dtype: int64
print("언더샘플링 적용후 종속변수 분포")
print(y_train_under["y1"].value_counts())
언더샘플링 적용후 종속변수 분포
y1
False 20530
True 20530
Name: count, dtype: int64
- 클래스 불균형 문제를 해결하기 위해 언더샘플링을 적용
list(x_train)
['BMI',
'PhysicalHealth',
'MentalHealth',
...
# 컬럼명 복구
x_train_under.columns = x_train.columns
y_train_under.columns = y_train.columns
x_train_under.head()

x_train_under.shape
(41060, 37)
x_test.shape
(79949, 37)
# 모델 학습
logi = LogisticRegression()
logi.fit(x_train_under, y_train_under)

print(logi.score(x_train_under, y_train_under))
print(logi.score(x_test, y_test))
0.7644179249878227
0.7494903000662922
# 계수값 확인
print(logi.coef_)
[[ 0.07812681 0.00740989 0.01517354 -0.0569881 0.37296029 -0.18396565
1.25705053 0.30254747 0.74117717 -0.11364318 0.13757743 0.32507719
0.74856926 0.92766633 1.3493028 1.69041699 1.94715393 2.1916422
2.50928999 2.70768367 3.05910533 -0.76368449 -0.50568593 -0.2940684
-0.26922156 -0.25808589 0.2043201 0.51937681 0.27661669 0.03025086
1.52578414 1.03761581 1.91997426 0.43381892 0.29534956 0.58444019
0.14760436]]
# 오류 해결을 위해 데이터 타입을 float로 변경
x_train_under = x_train_under.astype(float)
# statsmodels 라이브러리로 로지스틱 모델 학습
logi2 = sm.Logit(y_train_under, x_train_under)
result = logi2.fit()
Optimization terminated successfully.
Current function value: 0.501118
Iterations 7
result.summary()

# coef: 기울기
# 로지스틱 회귀의 오즈비 확인
np.exp(logi.coef_)
array([[ 1.08125976, 1.00743741, 1.01528924, 0.94460531, 1.45202669,
0.83196438, 3.51503869, 1.35330192, 2.09840424, 0.89257639,
1.14749055, 1.38413748, 2.1139733 , 2.52860136, 3.85473708,
5.42174103, 7.00871187, 8.94989854, 12.29619657, 14.99450305,
21.30848455, 0.46594649, 0.60309175, 0.74522552, 0.76397397,
0.77252887, 1.22669075, 1.68097975, 1.31866082, 1.03071307,
4.59874821, 2.82247966, 6.82078292, 1.5431394 , 1.34359595,
1.79398641, 1.15905424]])
result.params
BMI 0.087499
PhysicalHealth 0.006102
MentalHealth 0.006020
SleepTime -0.068517
Smoking_Yes 0.349063
AlcoholDrinking_Yes -0.210271
Stroke_Yes 1.245506
DiffWalking_Yes 0.276822
Sex_Male 0.660377
AgeCategory_25-29 -1.271849
AgeCategory_30-34 -1.030911
AgeCategory_35-39 -0.792743
AgeCategory_40-44 -0.399342
AgeCategory_45-49 -0.208285
AgeCategory_50-54 0.224675
AgeCategory_55-59 0.571438
AgeCategory_60-64 0.834615
AgeCategory_65-69 1.086579
AgeCategory_70-74 1.400997
AgeCategory_75-79 1.605469
AgeCategory_80 or older 1.932453
Race_Asian -2.818775
Race_Black -2.533232
Race_Hispanic -2.375967
Race_Other -2.309628
Race_White -2.284929
Diabetic_No, borderline diabetes 0.208379
Diabetic_Yes 0.512654
Diabetic_Yes (during pregnancy) 0.118510
PhysicalActivity_Yes -0.121022
GenHealth_Fair 1.290777
GenHealth_Good 0.795862
GenHealth_Poor 1.703415
GenHealth_Very good 0.200574
Asthma_Yes 0.233243
KidneyDisease_Yes 0.574981
SkinCancer_Yes 0.167291
dtype: float64
np.exp(result.params)
BMI 1.091441
PhysicalHealth 1.006121
MentalHealth 1.006039
SleepTime 0.933777
Smoking_Yes 1.417739
AlcoholDrinking_Yes 0.810364
Stroke_Yes 3.474693
DiffWalking_Yes 1.318931
Sex_Male 1.935521
AgeCategory_25-29 0.280313
AgeCategory_30-34 0.356682
AgeCategory_35-39 0.452601
AgeCategory_40-44 0.670761
AgeCategory_45-49 0.811976
AgeCategory_50-54 1.251915
AgeCategory_55-59 1.770812
AgeCategory_60-64 2.303926
AgeCategory_65-69 2.964116
AgeCategory_70-74 4.059246
AgeCategory_75-79 4.980195
AgeCategory_80 or older 6.906429
Race_Asian 0.059679
Race_Black 0.079402
Race_Hispanic 0.092925
Race_Other 0.099298
Race_White 0.101781
Diabetic_No, borderline diabetes 1.231679
Diabetic_Yes 1.669717
Diabetic_Yes (during pregnancy) 1.125818
PhysicalActivity_Yes 0.886014
GenHealth_Fair 3.635609
GenHealth_Good 2.216351
GenHealth_Poor 5.492672
GenHealth_Very good 1.222104
Asthma_Yes 1.262688
KidneyDisease_Yes 1.777097
SkinCancer_Yes 1.182098
dtype: float64
- 독립변수가 종속변수의 심장병 여부 확률에 어떤 영향을 미치는지 확인하기 위해 오즈비를 산출
- 해당 독립변수가 1일 때 심장병 발생 확률이 몇 배 더 큰지를 나타냄
- 예) Smoking_Yes 변수의 오즈비는 1.4이기 때문에 흡연자는 비흡연자보다 심장병 발생 확률이 1.4배 높다
728x90
'08_ML(Machine_Learning)' 카테고리의 다른 글
| 19_의사 결정 나무 (2) | 2025.04.09 |
|---|---|
| 18_확률적 경사 하강법 (0) | 2025.04.09 |
| 15_로지스틱 감성분류(자연어 처리) - 맛집 리뷰 (6) | 2025.04.08 |
| 14_로지스틱 회귀 (0) | 2025.04.07 |
| 12_야구선수 연봉_선형회귀 (1) | 2025.04.04 |