728x90
탐색적 데이터 분석
- 국가별 음주 데이터 분석
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

...
데이터 파악
drinks = pd.read_csv("./data/drinks.csv")
drinks.head()
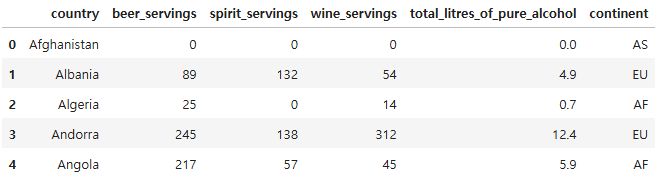
drinks.shape
(193, 6)
drinks.dtypes
country object
beer_servings int64
spirit_servings int64
wine_servings int64
total_litres_of_pure_alcohol float64
continent object
dtype: object
drinks.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 193 entries, 0 to 192
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 country 193 non-null object
1 beer_servings 193 non-null int64
2 spirit_servings 193 non-null int64
3 wine_servings 193 non-null int64
4 total_litres_of_pure_alcohol 193 non-null float64
5 continent 170 non-null object
dtypes: float64(1), int64(3), object(2)
memory usage: 9.2+ KB
drinks.describe()
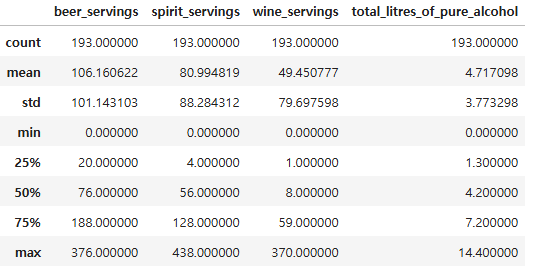
- 피처
- country: 국가 정보
- beer/spirit/wine servings : beer/spirit/wine 소비량
- total_litres_of_pure_alcohol : 총 알코올 소비량
- continent: 국가의 대륙 정보
데이터 속성 탐색
- 상관 분석
- 두 변수 간의 선형적 관계를 상관 계수로 표현하는 것(상관계수가 0.3~0.7사이의 값이면 관계가 있다고 볼 수 있음)
- 상관계수는 공분산의 개념을 포함함
- 공분산
- 2개의 확률변수에 대한 상관 정도
- 2개의 변수 중 하나의 값이 상승하는 경향을 보일 때 다른 값도 상승하는 경향을 수치로 나타낸 것
- 공분산 만으로 상관관계를 구한다면 두 변수의 단위 크기에 영향을 받음
- 큰 단위의 데이터라면 공분산이 커짐
- 공분산
- 따라서 상관계수는 공분산을 -1과 1사이의 값으로 변환한 것
- 상관관계를 통계적으로 탐색하는 방법
- 단순 상관 분석: 피처가 2개일 때의 상관 계수를 계산
- 다중 상관 분석: 피처가 여러개 일 때 상호간의 연관성 분석
beer_servings, wine_servings 의 상관 계수 구하기
drinks[["beer_servings", "wine_servings"]].corr() # corr()로 상관계수를 구할 수 있다
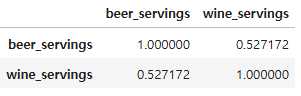
다중 상관 분석
drinks.columns
Index(['country', 'beer_servings', 'spirit_servings', 'wine_servings',
'total_litres_of_pure_alcohol', 'continent'],
dtype='object')
cor_cols = drinks.columns[1:5]
cor_cols
Index(['beer_servings', 'spirit_servings', 'wine_servings',
'total_litres_of_pure_alcohol'],
dtype='object')
drinks_corr = drinks[cor_cols].corr()
drinks_corr
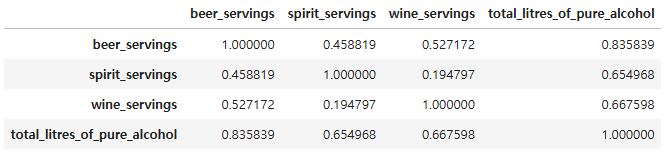
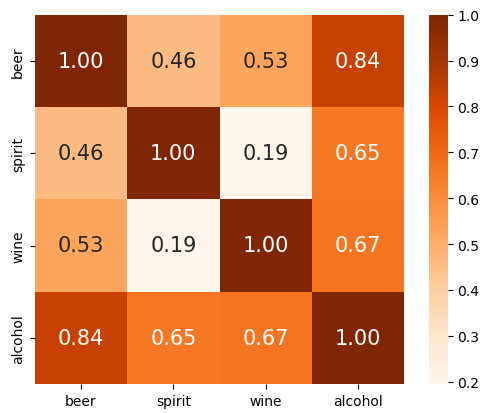
heatmap 시각화
# 그래프 출력을 위해 컬럼명 축약
cols_label = ["beer", "spirit", "wine", "alcohol"]
sns.heatmap(drinks_corr.values, cbar = True, annot = True, square = True, fmt = ".2f",
annot_kws = {"size" : 15}, yticklabels = cols_label, xticklabels = cols_label,
cmap = "Oranges")
plt.show()
산점도 시각화
sns.pairplot(drinks[cor_cols])
plt.show()
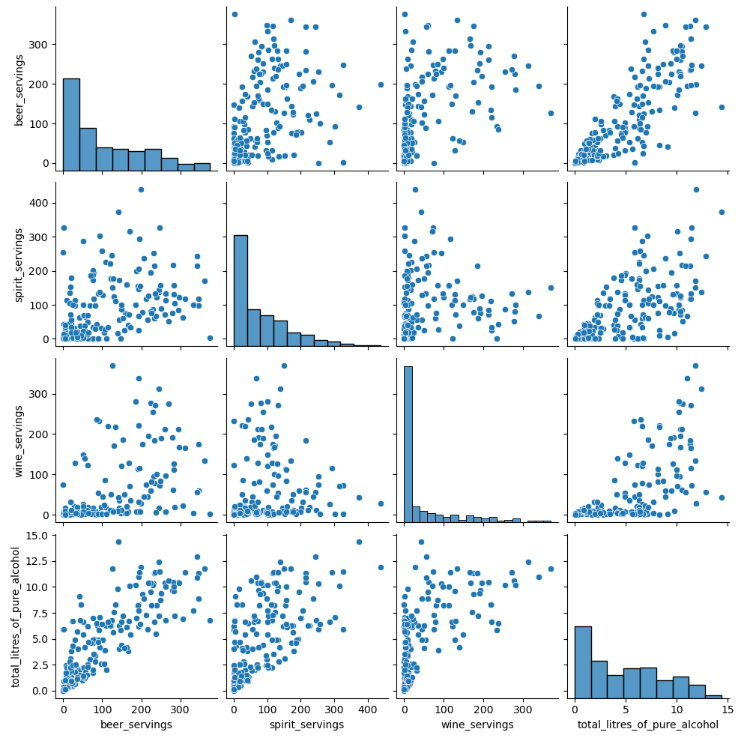
- total_litres_of_pure_alcohol 피처가 대체적으로 다른 모든 피처와 강한 상관관계가 있는 것으로 보임
- 특히 beer_servings 와의 상관성이 가장 높음
데이터 전처리
continent 결측치 대체
drinks.isna().sum()
country 0
beer_servings 0
spirit_servings 0
wine_servings 0
total_litres_of_pure_alcohol 0
continent 23
dtype: int64
drinks["continent"].unique()
array(['AS', 'EU', 'AF', nan, 'SA', 'OC'], dtype=object)drinks[drinks["continent"] == "SA"] # South America가 있는데 North America가 없음
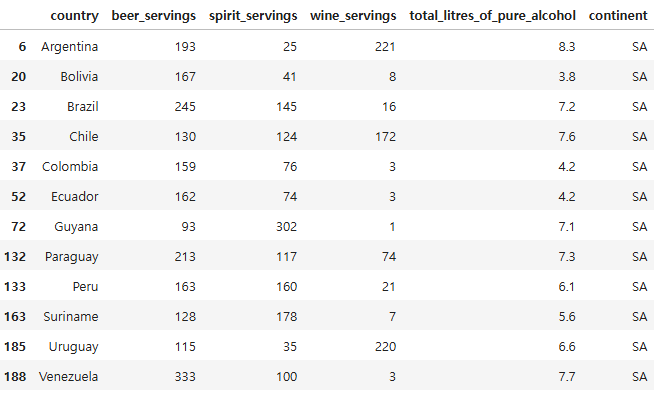
drinks[drinks["continent"].isna()]
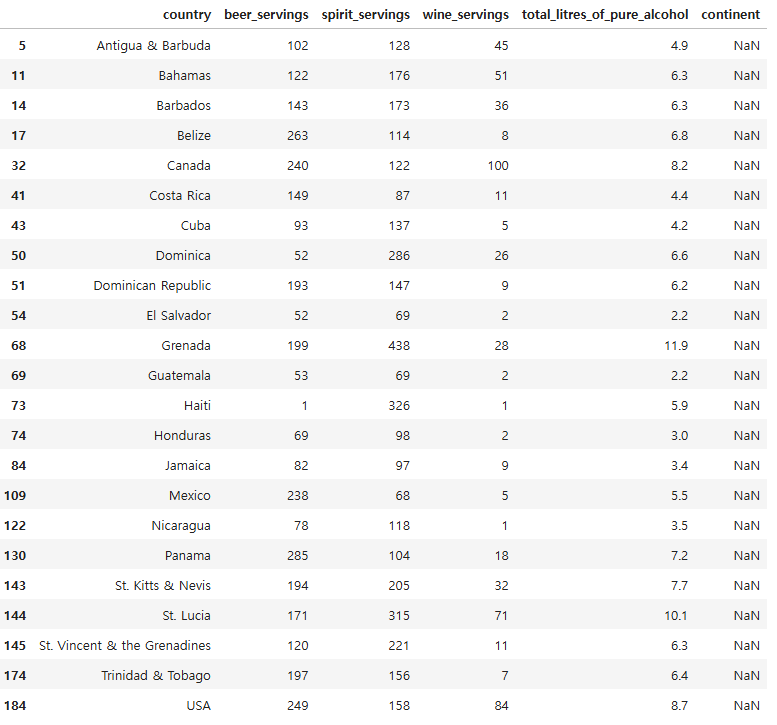
drinks["continent"] = drinks["continent"].fillna("NA")
drinks["continent"].value_counts()
continent
AF 53
EU 45
AS 44
NA 23
OC 16
SA 12
Name: count, dtype: int64
데이터 탐색
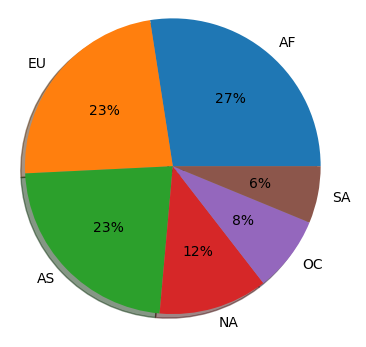
각 대륙별 비율 확인
continents = drinks["continent"].value_counts()
plt.pie(continents.values, labels = continents.index, autopct = "%.0f%%", shadow = True)
plt.show()
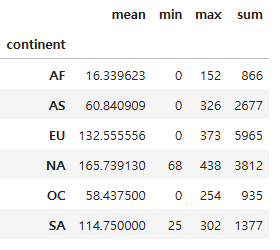
대륙별 spirit_servings의 통계 정보 확인
# 대륙별 spirit_servings의 평균, 최소, 최대, 합계 확인
stat = drinks.groupby("continent")["spirit_servings"].agg(["mean", "min", "max", "sum"])
stat
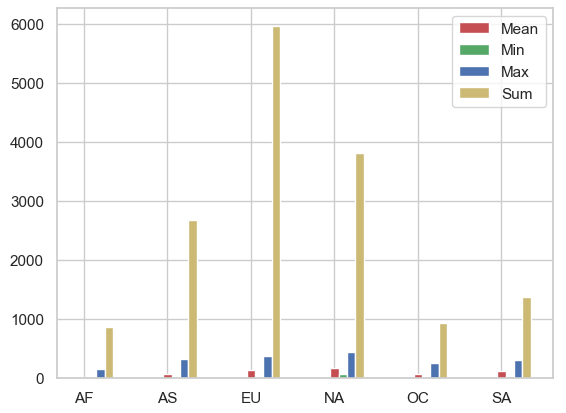
# seaborn의 색감 설정
sns.set(style = "whitegrid")
n_groups = len(stat)
idx = np.arange(n_groups)
rects1 = plt.bar(idx, stat["mean"], width = 0.1, color = "r", label = "Mean")
rects2 = plt.bar(idx + 0.1 , stat["min"], width = 0.1, color = "g", label = "Min")
rects3 = plt.bar(idx + 0.2 , stat["max"], width = 0.1, color = "b", label = "Max")
rects4 = plt.bar(idx + 0.3 , stat["sum"], width = 0.1, color = "y", label = "Sum")
plt.xticks(idx, stat.index)
plt.legend()
plt.show()
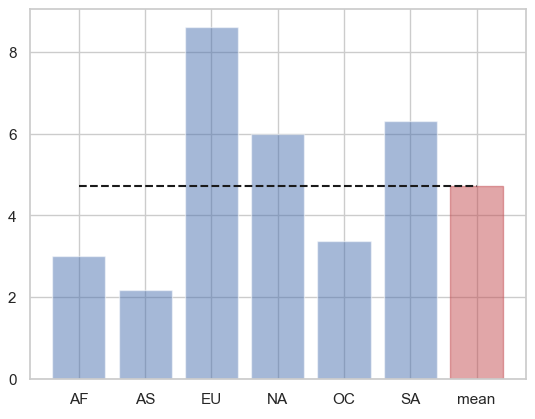
전체 평균보다 더 많은 알코올을 섭취하는 대륙
alc_mean = drinks["total_litres_of_pure_alcohol"].mean()
alc_mean
4.717098445595855con_mean = drinks.groupby("continent")["total_litres_of_pure_alcohol"].mean()
con_mean
continent
AF 3.007547
AS 2.170455
EU 8.617778
NA 5.995652
OC 3.381250
SA 6.308333
Name: total_litres_of_pure_alcohol, dtype: float64
con_mean[con_mean > alc_mean]
continent
EU 8.617778
NA 5.995652
SA 6.308333
Name: total_litres_of_pure_alcohol, dtype: float64
# 전체 평균도 시각화해주기 위해서 대륙 리스트에 mean 추가
continents = con_mean.index.tolist()
continents.append("mean")
alc = con_mean.tolist()
alc.append(alc_mean)
# x_pos = np.arange(len(con_mean))
x_pos = np.arange(len(continents))
# plt.bar(x_pos, con_mean, alpha = 0.5)
bar_list = plt.bar(x_pos, alc, alpha = 0.5)
# 마지막 바 만 빨간색으로 변경
bar_list[-1].set_color("r")
# 평균선 그리기
plt.plot([0, len(continents) - 1], [alc_mean, alc_mean], "k--")
# plt.xticks(x_pos, con_mean.index)
plt.xticks(x_pos, continents)
plt.show()
continents
['AF', 'AS', 'EU', 'NA', 'OC', 'SA', 'mean']
con_mean.tolist()
[3.0075471698113208,
2.1704545454545454,
8.617777777777778,
5.995652173913044,
3.38125,
6.308333333333334]
평균 beer_servings가 가장 높은 대륙
drinks.groupby("continent")["beer_servings"].mean()
continent
AF 61.471698
AS 37.045455
EU 193.777778
NA 145.434783
OC 89.687500
SA 175.083333
Name: beer_servings, dtype: float64# 최댓값의 인덱스
drinks.groupby("continent")["beer_servings"].mean().idxmax()
'EU'
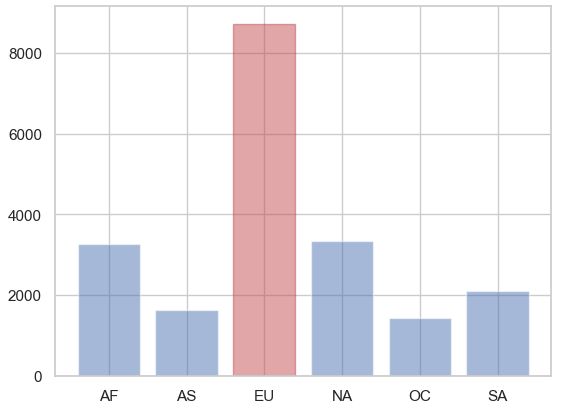
group_beer = drinks.groupby("continent")["beer_servings"].sum()
group_beer
continent
AF 3258
AS 1630
EU 8720
NA 3345
OC 1435
SA 2101
Name: beer_servings, dtype: int64
continents.index("EU")
2
continents = group_beer.index.tolist()
x_pos = np.arange(len(group_beer))
bar_list = plt.bar(x_pos, group_beer, alpha = 0.5)
bar_list[continents.index("EU")].set_color("r")
plt.xticks(x_pos, continents)
plt.show()
통계 분석
- 지금까지의 분석은 통찰을 발견하는 데 있어서는 유용했지만 분석가의 주관에 따라 분석된 내용이기 때문에 타당성을 입증하기 어려움
- 타당성을 위해서는 통계적으로 검정하는 과정이 필요
- t검정(t-test)
- 두 집단 간 평균의 차이에 대한 검정
- 모집단의 평균을 모를 때 현재의 데이터만으로 두 집단의 차이에 대해 검정할 수 있음
- 단, 두 집단의 데이터 개수가 비슷하고, 정규 분포인 경우에 신뢰도가 높음
- 정규성 검정
- 등분산성 검정(데이터가 퍼져있는 정도가 두 집단이 같은가)
- T-test
아프리카와 유럽 간의 맥주 소비량 차이 검정
# 파이썬에서 통계를 쓸 때 scipy를 많이 씀
from scipy import stats
af = drinks[drinks["continent"] == "AF"]
eu = drinks[drinks["continent"] == "EU"]
# 정규성 검정
af_shapiro = stats.shapiro(af["beer_servings"])
eu_shapiro = stats.shapiro(eu["beer_servings"])
print(af_shapiro)
print(eu_shapiro)
ShapiroResult(statistic=0.6982116200099862, pvalue=3.84314570688321e-09)
ShapiroResult(statistic=0.9592717067348022, pvalue=0.1145794783307496)# 등분산성 검정
levene_result = stats.levene(af["beer_servings"], eu["beer_servings"])
levene_result
LeveneResult(statistic=6.015144059118397, pvalue=0.015989187968374834)# H0 : 정규성 만족, 등분산성 만족
# H1 : 정규성 만족X, 등분산성 만족X
# t-test
t_result = stats.ttest_ind(af["beer_servings"], eu["beer_servings"], equal_var = False)
t_result
TtestResult(statistic=-7.143520192189803, pvalue=2.9837787864303205e-10, df=84.40013075489844)
- statistic(t-test의 검정 통계량) : 절댓값이 클수록 두 집단간의 평균이 크다
- 그 자체로는 아무 의미 없으며 p-value 와 함께 해석해야함
- 귀무가설과의 차이를 뜻함
- p-value(유의확률)
- 가설이 얼마나 믿을만 한 것인지를 나타내는 지표
- 데이터를 새로 샘플링했을 때 귀무 가설이 맞다는 전제 하에 현재 나온 통계값 이상이 나올 확률
- 즉, p-value가 낮으면 귀무 가설이 일어날 확률이 낮기 때문에 귀무 가설을 기각하게 됨
- 보통 그 기준은 0.05나 0.01을 기준으로 함
- 즉, p-value가 낮으면 귀무 가설이 일어날 확률이 낮기 때문에 귀무 가설을 기각하게 됨
- 귀무가설
- 처음부터 버릴 것을 예상하는 가설
- 가설이 맞지 않다는 것을 증명하기 위해 수립하는 가설
- 반대되는 가설을 대립 가설이라고 부르며, 귀무 가설이 거짓인 경우에 대안으로 참이 되는 가설임
분석 내용
- t-test 의 귀무가설 : "두 집단의 평균이 같다"
- p-value가 0.01이하로 나타나 귀무 가설이 기각되었음
- 따라서 "아프리카와 유럽 대륙 간의 맥주 소비량 차이"는 통계적으로 매우 유의미하다
- 두 집단의 평균은 다르다
728x90
'07_Data_Analysis' 카테고리의 다른 글
| 13_T-Test (0) | 2025.03.19 |
|---|---|
| 12_T-Test, ANOVA 개요 (0) | 2025.03.19 |
| 10_탐색적 데이터 분석 (0) | 2025.03.19 |
| 09_데이터 분석의 이해 (4) | 2025.03.17 |
| 08_분포 시각화 (0) | 2025.03.17 |