09_DL(Deep_Learning)

19_파이토치_기초문법

chuuvelop 2025. 5. 2. 21:49

728x90

파이토치_기초문법

텐서

파이토치는 텐서로 시작해서 텐서로 끝남
텐서를 잘 다룰 수 있어야 신경망에서 데이터 입력과 출력을 제어할 수 있음

# 파이토치 설치
# https://pytorch.org/
# Stable(2.7.0)>Windows>Pip>Python>CPU
# pip3 install torch torchvision torchaudio

import torch

텐서 생성 및 변환

텐서는 파이토치의 가장 기본이 되는 데이터 구조
numpy의 다차원배열과 비슷하며 GPU에서도 연산 가능

# 2차원 텐서 생성
torch.tensor([[1, 2], [3, 4]])

tensor([[1, 2],
        [3, 4]])

# gpu가 있다면
# torch.tensor([[1, 2], [3, 4]], device = "cuda:0") # cuda의 0번째 메모리를 쓰라

# dtype을 이용하여 텐서 생성
torch.tensor([[1, 2], [3, 4]], dtype = torch.float64)

tensor([[1., 2.],
        [3., 4.]], dtype=torch.float64)

텐서를 ndarray로 변환

temp = torch.tensor([[1, 2], [3, 4]])

# ndarray로 변환
temp.numpy()

array([[1, 2],
       [3, 4]], dtype=int64)

# gpu가 있다면
# gpu상의 텐서를 cpu의 텐서로 변환한 후 ndarray로 변환
# temp = torch.tensor([[1, 2], [3, 4]], device = "cuda:0")
# temp.to("cpu").numpy() # numpy는 그래픽카드에서 연산이 안되므로 cpu에 옮겨서 numpy로 변환을 해야함

텐서의 인덱스 조작

텐서는 넘파이의 다차원배열과 유사하게 동작하기 때문에 배열처럼 인덱스를 바로 지정하거나 슬라이싱 등을 사용할 수 있음

# 파이토치로 1차원 벡터 생성
temp = torch.FloatTensor([1, 2, 3, 4, 5, 6, 7])

# 인덱스로 접근
temp[0], temp[1], temp[-1]

(tensor(1.), tensor(2.), tensor(7.))

# 슬라이싱
temp[2:5], temp[4:-1]

(tensor([3., 4., 5.]), tensor([5., 6.]))

텐서 연산

텐서는 넘파이의 다차원배열처럼 다양한 수학 연산이 가능하며, gpu를 사용하면 더 빠르게 연산할 수 있음
단, 텐서 간의 타입이 다르면 연산이 불가
- 예) FloatTensor(32비트의 부동 소수점)와 DoubleTensor(64비트의 부동소수점) 간에 사칙 연산을 수행하면 오류 발생

# 길이가 3인 벡터 생성
v = torch.tensor([1, 2, 3])
w = torch.tensor([3, 4, 6])

# 길이가 같은 벡터 간 뺄셈 연산
print(w - v)

tensor([2, 2, 3])

텐서의 차원 조작

텐서의 차원을 변경하는 명령어
- view : 넘파이의 reshape와 유사
- cat : 다른 길이의 텐서를 하나로 병합
- transpose : 행렬의 전치 또는 차원의 순서 변경

# 2 X 2 행렬 생성
temp = torch.tensor([[1, 2], [3, 4]])

temp.shape

torch.Size([2, 2])

# 4 X 1 로 변경
temp.view(4, 1)

tensor([[1],
        [2],
        [3],
        [4]])

temp.view(-1)

tensor([1, 2, 3, 4])

temp.view(1, -1)

tensor([[1, 2, 3, 4]])

temp.view(-1, 1)

tensor([[1],
        [2],
        [3],
        [4]])

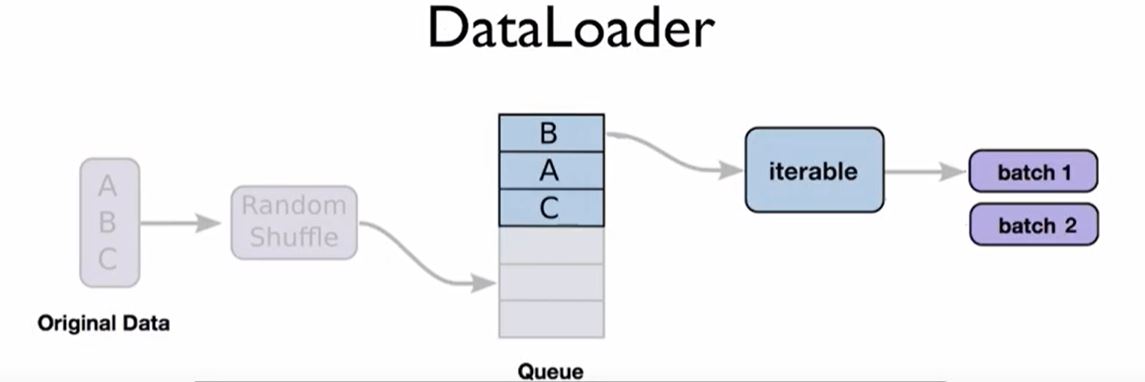
데이터로더

# 스택: 후입선출

# 큐: 선입선출

torch.utils.data.DataLoader 는 학습에 사용될 데이터 전체를 보관했다가 모델 학습을 할 때 배치 크기만큼 데이터를 꺼내서 사용
주의할 점은 미리 데이터를 잘라 놓는 것이 아니라 내부적으로 이터레이터에 포함된 인덱스를 이용하여 배치크기 만큼 데이터를 반환

파이토치 데이터셋 사용

torchvision은 파이토치에서 제공하는 데이터셋이 모여있는 패키지
파이토치 데이터셋을 다운로드 받으려면 requests 라이브러리 설치가 필요
- HTTP 요청을 하기 위함

import torchvision.transforms as transforms
from torchvision.datasets import MNIST

# 평균이 0.5, 표준편차가 1.0이 되도록 데이터의 분포를 정규화
mnist_transforms = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (1.0,))
])

data_path = "./data/MNIST_DATASET"

train_dataset = MNIST(data_path, transform = mnist_transforms, train = True, download = True)
test_dataset = MNIST(data_path, transform = mnist_transforms, train = False, download = True)

모델 정의

파이토치에서 모델을 정의하기 위해서는 module을 상속한 클래스를 사용
- layer : 모듈 또는 모듈을 구성하는 한 개의 계층
  - 예) 합성곱층, 선형계층 등
- module : 한 개 이상의 계층이 모여서 구성된 것, 모듈이 모여 새로운 모듈을 만들 수도 있음

nn.Module() 을 상속하여 정의하는 방법

파이토치에서 nn.Module을 상속받는 모델은 기본적으로 __init__() 과 forward() 함수를 포함
__init__() 에서는 모델에서 사용될 모듈, 활성화 함수 등을 정의
forward() 함수에서는 모델에서 실행되어야 하는 연산을 정의
nn.Sequential을 사용하면 init() 에서 사용할 네트워크 모델들을 정의해줄 뿐만 아니라 forward() 함수에서 실행되어야 할 계산을 좀 더 가독성이 뛰어나게 코드로 작성할 수 있음
또한, Sequential 객체에는 그 안에 포함된 각 모듈을 순차적으로 실행해 줌

import torch.nn as nn

class MLP(nn.Module):
    def __init__(self):
        # python2에서는 이렇게 작성했었으나, 3에서는 필요없음
        # super(MLP, self).__init__()
        super().__init__()
        self.layer1 = nn.Sequential(
            # 입력되는 채널수 1 / 출력 64/ 커널 수 5 -> 숫자 맞춰줘야함
            nn.Conv2d(in_channels = 1, out_channels = 64, kernel_size = 5),
            # inplace = True : input으로 들어온 값 자체를 수정
            # 메모리 효율이 좋아지지만 input값이 사라짐
            nn.ReLU(inplace = True),
            nn.MaxPool2d(2)
        )

        self.layer2 = nn.Sequential(
            nn.Conv2d(in_channels = 64, out_channels = 30, kernel_size = 5), # (28, 28, 1)
            nn.ReLU(inplace = True), #(26, 26, kernnel)
            nn.MaxPool2d(2) # (13, 13, kernel)
        )

        self.layer3 = nn.Sequential(
            nn.Linear(in_features = 750, out_features = 10, bias = True), #(11, 11, 30)
            nn.ReLU(inplace = True) #(5, 5, 30)
            # 5 * 5 * 30 = 750
        )

    def forward(self, x):
        x = self.layer1(x)
        x = self.layer2(x)
        x = x.view(x.shape[0], -1)
        x = self.layer3(x)
        return x

# 모델 객체 생성
model = MLP()

list(model.children())

[Sequential(
   (0): Conv2d(1, 64, kernel_size=(5, 5), stride=(1, 1))
   (1): ReLU(inplace=True)
   (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
 ),
 Sequential(
   (0): Conv2d(64, 30, kernel_size=(5, 5), stride=(1, 1))
   (1): ReLU(inplace=True)
   (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
 ),
 Sequential(
   (0): Linear(in_features=750, out_features=10, bias=True)
   (1): ReLU(inplace=True)
 )]

# 모든 노드들을 반환
list(model.modules())

[MLP(
   (layer1): Sequential(
     (0): Conv2d(1, 64, kernel_size=(5, 5), stride=(1, 1))
     (1): ReLU(inplace=True)
     (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
   )
   (layer2): Sequential(
     (0): Conv2d(64, 30, kernel_size=(5, 5), stride=(1, 1))
     (1): ReLU(inplace=True)
     (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
   )
   (layer3): Sequential(
     (0): Linear(in_features=750, out_features=10, bias=True)
     (1): ReLU(inplace=True)
   )
 ),
 Sequential(
   (0): Conv2d(1, 64, kernel_size=(5, 5), stride=(1, 1))
   (1): ReLU(inplace=True)
   (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
 ),
 Conv2d(1, 64, kernel_size=(5, 5), stride=(1, 1)),
 ReLU(inplace=True),
 MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False),
 Sequential(
   (0): Conv2d(64, 30, kernel_size=(5, 5), stride=(1, 1))
   (1): ReLU(inplace=True)
   (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
 ),
 Conv2d(64, 30, kernel_size=(5, 5), stride=(1, 1)),
 ReLU(inplace=True),
 MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False),
 Sequential(
   (0): Linear(in_features=750, out_features=10, bias=True)
   (1): ReLU(inplace=True)
 ),
 Linear(in_features=750, out_features=10, bias=True),
 ReLU(inplace=True)]

함수로 신경망 정의

# 클래스 방식으로 정의하는것이 더 좋으나 함수로 정의해봄
def MLP(in_features = 1, hideen_features = 20, out_features = 1):
    hidden = nn.Linear(in_features = in_features, out_features = hidden_features, bias = True)
    activation = nn.ReLU()
    output = nn.Linear(in_features = hidden_features, out_features = out_features, bias = True)
    net = nn.Sequential(hidden, activation, output)
    return net

모델 파라미터 정의

손실 함수(loss function)
- 학습하는 동안 출력과 실제 값(정답) 사이의 오차를 측정
- wx + b 를 계산한 값과 실제값 y의 오차를 구해서 모델의 정확성을 측정
- 자주 사용되는 손실 함수
  - BCELoss : 이진 분류를 위해 사용
  - CrossEntropyLoss : 다중 클래스 분류를 위해 사용
  - MSELoss : 회귀 모델에서 사용
옵티마이저(optimizer)
- 데이터와 손실 함수를 바탕으로 모델의 업데이트 방법을 결정
- 옵티마이저의 주요 특성
  - optimizer는 step() 메서드를 통해 전달받은 파라미터를 업데이트
  - 모델의 파라미터별로 다른 기준을 적용시킬 수 있음
  - torch.optim.Optimizer(params, defaults)는 모든 옵티마이저의 기본이 되는 클래스
  - zero_grad() 메서드는 옵티마이저에 사용된 파라미터들의 기울기를 0으로 초기화
  - torch.optim.lr_scheduler는 에포크에 따라 학습률을 조절할 수 있음
학습률 스케줄러(learning rate scheduler)
- 미리 지정한 횟수의 에포크를 지날 때마다 학습률을 감소시킴
- 학습률 스케줄러를 이용하면 학습 초기에는 빠른 학습을 진행하다가 전역 최소점(global minimum) 근처에 다다르면 학습률을 줄여서 최적점을 찾아갈 수 있도록 함
- 학습률 스케줄러의 종류
  - optim.lr_scheduler.LambdaLR : 람다 함수를 이용하여 그 함수의 결과를 학습률로 설정
  - optim.lr_scheduler.StepLR : 특정 단계(step)마다 학습률을 감마 비율만큼 감소
  - optim.lr_scheduler.MultiStepLR : StepLR과 비슷하지만 특정 단계가 아닌 지정된 에포크에만 감마 비율을 감소시킴
  - optim.lr_scheduler.ExponentialLR : 에포크마다 이전 학습률에 감마만큼 곱함
  - optim.lr_scheduler.CosineAnnealingLR : 학습률을 코사인 함수의 형태처럼 변화시킴, 학습률이 커지기도 작아지기도 함
  - optim.lr_scheduler.ReduceLROnPlateau : 학습이 잘 되고 있는지 아닌지에 따라 동적으로 학습률을 변화
지표(metrics)
- 훈련과 테스트 단계를 모니터링

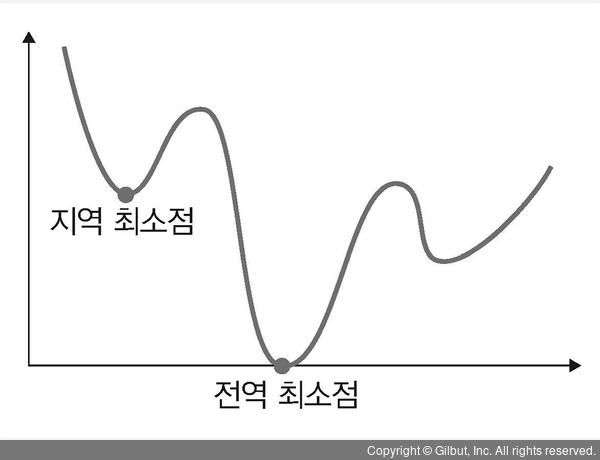
전역 최소점과 최적점

손실 함수는 실제 값과 예측값 차이를 수치화 해주는 함수
이 오차 값이 클수록 손실 함수의 값이 크고, 오차 값이 작을수록 손실 함수의 값이 작아짐
손실 함수의 값을 최소화하는 가중치와 바이어스를 찾는 것이 모델 학습의 목표
전역 최소점(global minimum)은 오차가 가장 작을 때의 값을 의미하므로 우리가 최종적으로 찾고자 하는 것. 최적점
지역 최소점(local minimum)은 전역 최소점을 찾아가는 과정에서 만나는 홀(hole)과 같은 것으로 옵티마이저가 지역 최소점에서 학습을 멈추면 최솟값을 찾는 오차를 찾을 수 없는 문제가 발생

모델 훈련

모델을 학습시킨다는 것은 y = wx + b 라는 함수에서 w와 b의 적절한 값을 찾는다는 의미
w와 b에 임의의 값을 적용하여 시작하며 오차가 줄어들어 전역 최소점에 이를 때까지 파라미터(w, b)를 계속 수정
딥러닝 학습 절차
1. 모델, 손실 함수, 옵티마이저 정의
2. 전방향 학습(입력 -> 출력 계산)
3. 손실 함수로 출력과 정답의 차이(오차) 계산
4. 역전파 학습(기울기 계산)
5. 기울기 업데이트
파이토치 학습 절차
1. 모델, 손실 함수, 옵티마이저 정의
  - optimizer.zero_grad() : 기울기 초기화
    - 파이토치는 기울기 값을 계산하기 위해 loss.backward() 메서드를 이용하는데, 이 때 새로운 기울기 값이 이전 기울기 값에 누적하여 계산됨
    - 기울기 누적은 필요한 경우도 있지만 모델에 따라서는 불필요할 수 있음
    - 따라서 기울기 누적 계산이 필요하지 않을 때는 입력 값을 모델에 적용하기 전에 미분값이 누적되지 않게 초기화 해야함
2. output = model(input) : 출력 계산
3. loss = loss_fn(output, target) : 오차 계산
4. loss.backward() : 역전파 학습
5. optimizer.step() : 기울기 업데이트

728x90